Problema d'optimització (con inscrit en con)
ENUNCIAT DEL PROBLEMA
En un con de revolució de 30 cm d’altura i 10 cm de radi s’hi ha inscrit un altre con de revolució amb el vèrtex invertit al del con exterior. Determineu quines han de ser les dimensions del con interior per tal que el seu volum sigui màxim i calculeu aquest volum.
PLANTEJAMENT
Per facilitar la representació, suposarem que el con exterior té la base sobre el pla XY (és a dir, el pla de l'espai 3D on tots els punts tenen com a tercera coordenada ) i que el con està orientat cap al semiespai positiu (podeu veure-ho a la figura que hi ha més avall). Com que l'altura del con és de 30 cm, el vèrtex del con és el punt .
La base del con interior és paral·lela a la base del con exterior, i el seu centre es desplaça sobre l'eix del con (és el segment que uneix els punts i . Sabem que la fórmula del volum d'un con de revolució és:
Designarem l'altura d'aquest con interior amb la lletra , de tal manera que . Per trobar el radi de la base, és suficient determinar la distància d'un punt de la circumferència de la base del con interior a l'eix del con exterior. Es pot veure a la següent imatge:
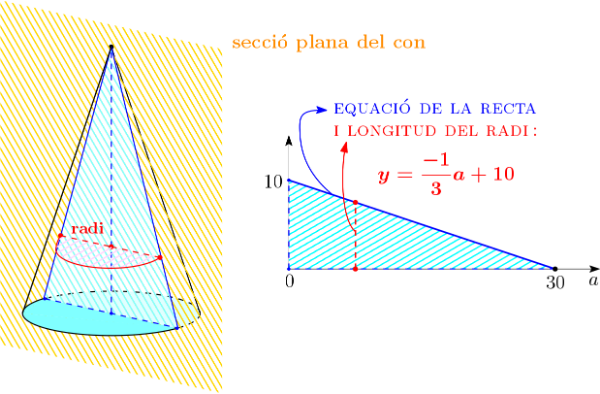
Per tant, i . Deduïm que la funció objectiu (és a dir, la funció que hem d'optimitzar) és:
Si ho simplifiquem obtenim: