Produktregel
Quelle: http://www.riemer-koeln.de/mathematik/publikationen/pm-produktregel/pm-produktregel.pdf
u hat der Stelle 4 den Funktionswert a=2 und die Steigung m=0,5.
v hat dort den Funktionswert b=3 und die Steigung n=1.
Das Produkt f=u*v hat dann an der Stelle 4 den Funktionswert a*b=6.
So ist das Produkt zweier Funktionen definiert.
Aber wie groß ist dort die Steigung s?
Sie lässt sich aus a, b, m und n berechnen.
Finden Sie heraus wie ...
und anschließend warum!
1. Entdecken
Variieren Sie die vier Parameter a=u(4) , b=v(4) , m=u’(4) und n=v’(4) systematisch und halten Sie
fest, wie sich s dabei verändert. Dokumentieren Sie Ihre Ergebnisse in einer Tabelle.
Drücken Sie s durch a, b, m und n mithilfe eines Terms aus: s = .... .
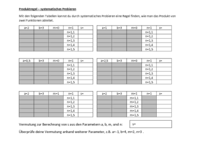
Tipps zum systematischen Probieren
2. Kontrollieren
Wenn Ihre Entdeckung stimmt, enthält sie die Faktorregel (c*f)’=c*f’ für einen konstanten Faktor c
als Spezialfall. Erläutern und begründen Sie!
3. Begründen an einem Spezialfall
Nehmen Sie an:
- u ist eine lineare Funktion, deren Graph durch (4;a) verläuft und die Steigung m hat
- v ist eine lineare Funktion, deren Graph durch (4;b) verläuft und die Steigung n besitzt.
Diese Annahmen machen Sinn, denn Sie wissen: Jede Funktion sieht lokal wie eine Gerade aus.
Beschreiben Sie in Worten, was sie sehen – und kontrollieren Sie Ihre
Endeckung aus 1 rechnerisch.
4. Begründen allgemein
Wenn man im ursprünglichen Applet von der Stelle 4 um h=0,01 nach rechts geht, wächst
- u von 2 auf 2+mh
- v von 3 auf 3+nh und
- f=u*v von 6 auf (2+mh)(3+nh)=6+(2*n+3*m)h+mnh².
Erläutern Sie in eigenen Worten, warum diese Umformung die Entdeckung aus 1 begründet.
Verallgemeinern Sie ... und formulieren Sie eine Regel zum Ableiten von Produktfunktionen