Conseguenze dell'assioma della parallela
Teorema: Transitività del parallelismo
Due rette distinte parallele a una terza retta sono parallele tra loro.
Ipotesi: r s, r t, s t
Tesi: r s
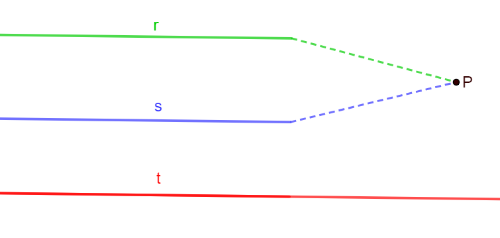
Dimostrazione per assurdo
Se r ed s si incontrassero in un punto P, per il punto P passerebbero due rette distinte entrambe parallele a t, ma l'assioma della parallela afferma che per un punto P passa una e una sola retta parallela a una retta data.
Quindi, supporre che le rette si incontrino in un punto è assurdo. Pertanto, le rette r ed s sono parallele.
La relazione di parallelismo è una relazione di equivalenza
Infatti:
- proprietà riflessiva: r r per definizione
- proprietà simmetrica: r s s r conseguenza della definizione
- proprietà transitiva: r s e s t r t per il teorema della transitività
Definizioni
Come ogni relazione di equivalenza, anche il parallelismo induce una partizione nell'insieme di tutte le rette. Si definisce direzione ogni classe di equivalenza in cui resta suddiviso l'insieme delle rette di un piano rispetto alla relazione di parallelismo.
L'insieme di tutte le rette che hanno una stessa direzione si dice fascio improprio di rette.
Si definisce fascio proprio di rette di centro P l'insieme di tutte le rette che passano per il punto P.
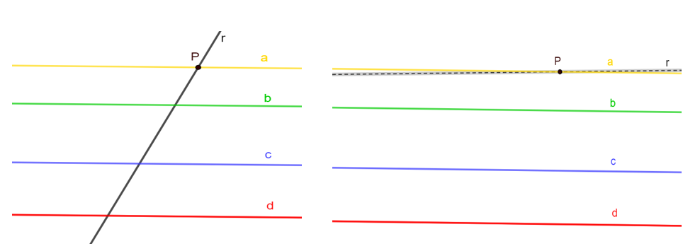
Teorema: rette incidenti a un fascio improprio
Se una retta r è incidente a una delle rette di un fascio improprio, allora è incidente anche a tutte le altre rette del fascio improprio.
Ipotesi: a b c ... ed r interseca a nel punto P
Tesi: r b , r c ... cioè, r interseca tutte le rette del fascio improprio
Dimostrazione per assurdo
Supponiamo che r non intersechi la retta b, cioè che r sia parallela a b, r b.
Allora per il punto P (intersezione della retta a con la retta r) passerebbero due rette parallele a b: a ed r.
Ma per l'assioma della parallela, per il punto P può passare una sola retta parallela a b ASSURDO
Quindi, r interseca b.
Lo stesso discorso si può ripetere per tutte le altre rette del fascio improprio e quindi, deduciamo che r interseca tutte le rette del fascio.