GeoGebra

Diagrama de Voronoi

Autor:Rafael Losada Liste
Esta actividad pertenece al libro de GeoGebra Voronoi Paintings. Imaginemos que marcamos dos puntos en el plano. Esos puntos pueden representar entes reales, como pozos de agua, estaciones de suministro, centros sanitarios, centros de comunicación, núcleos urbanos, etc. Para evitar posibles confusiones en el resto del artículo, llamaremos sitio a cada uno de estos puntos. Podemos preguntarnos cuál es la región del plano cuyos puntos están más próximos a un sitio que a otro. La respuesta es un semiplano, cuya frontera es la mediatriz entre ambos sitios. Ampliemos el número de sitios a una colección de n sitios. Tomemos un sitio cualquiera P de esa colección. ¿Cuál será ahora la región del plano cuyos puntos están más próximos a P que a ningún otro sitio de la colección? La respuesta es una intersección de semiplanos. Procediendo de igual modo para cada uno de los sitios, obtenemos una división del plano en n regiones excluyentes, denominadas regiones de Voronoi. Así, cada región de Voronoi está formada por todos los puntos más próximos a cada sitio de la colección dada. La frontera entre dos regiones colindantes es un trozo (segmento o semirrecta) de la mediatriz entre los sitios de la colección correspondientes a esas dos regiones. El conjunto de esos segmentos y semirrectas se denomina diagrama de Voronoi (Figura 1). Véase, por ejemplo, [7, 15] para una introducción elemental a este concepto.

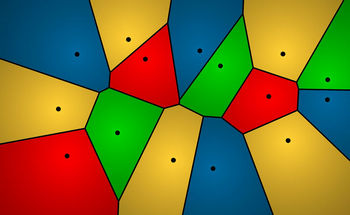
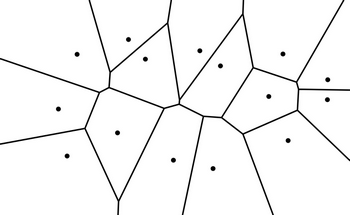
  Figura 1: Regiones y diagrama de Voronoi de una colección de 15 sitios

Observemos que cualquier punto del plano pertenece o bien al diagrama de Voronoi o bien a una única región de Voronoi. Dicho de otro modo, las regiones y el diagrama de Voronoi constituyen una partición del plano. GeoGebra dispone de un comando específico para crear el diagrama de Voronoi de una colección de sitios usando un sofisticado algoritmo interno. Alternativamente, podemos crear las regiones de Voronoi de una manera muy simple. Para cada sitio de la colección creamos una circunferencia de igual radio (regido por un deslizador) y suficientemente amplio para abarcar a toda la colección. A cada circunferencia le asignamos un color diferente y activamos su rastro. Finalmente, contraemos simultáneamente todas las circunferencias (animando el deslizador), hasta alcanzar sus centros. De este modo, cada punto del plano irá adquiriendo diferentes colores, según le vaya alcanzando el rastro de cada circunferencia, pero al finalizar el proceso el color “superviviente” siempre será el correspondiente al color de la circunferencia centrada en el sitio de la colección que se encuentre más próximo (véase [7] para una descripción interactiva con GeoGebra; y también [16], para un video ilustrativo). El comando de GeoGebra devuelve el diagrama de Voronoi en forma de grafo. Como tal, observemos que, en casi todos los casos, el grado de cada nodo es 3 (en los nodos concurren tres aristas) como ocurre en la Figura 1. Por casi todos entendemos la situación general, es decir, si tomamos sitios al azar, la probabilidad de que todos los nodos del diagrama de Voronoi correspondiente tengan grado 3 es 1. Recordemos que, con independencia del método empleado para la construcción del diagrama de Voronoi, en cualquier caso, ya sea general o no, un nodo queda determinado por aquellas intersecciones de mediatrices que son circuncentros de tres sitios, de modo que la circunferencia que pasa por ellos no contenga a ningún otro sitio en su interior.

Nuevos recursos

Descubrir recursos

Descubre temas