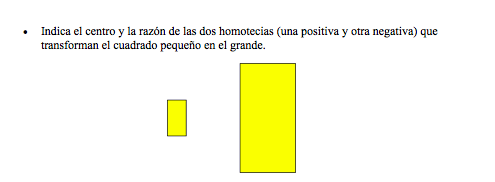
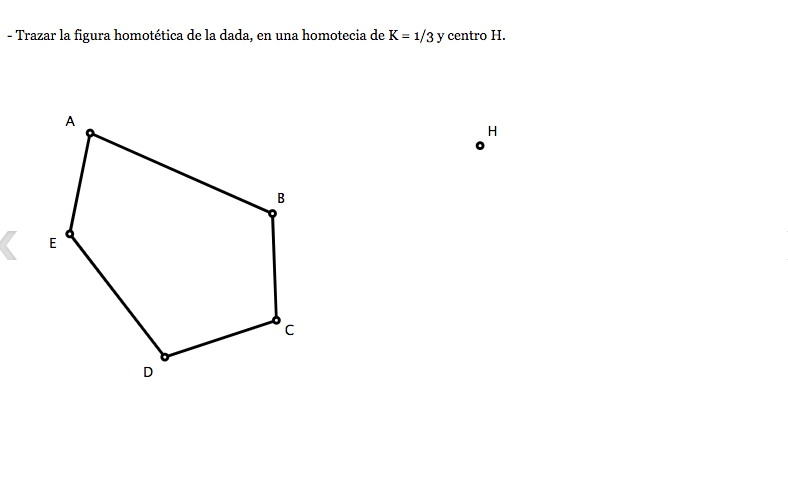
Copia de FIGURAS HOMOTÉTICAS
OBJETIVO
- Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
- Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
- Reconozcan homotecias de razones positivas y negativas.
- Compongan movimientos rígidos.
INTRODUCCIÓN
Se abordan en esta unidad conceptos elemental sobre homotecia y algunos enunciados referidos al teorema de Tales desprovistos del rigor de las demostraciones pero con la ventaja de poder comprobar sus conclusiones y propiedades de manera sencilla. Como conclusión se plantean los casos de semejanza de triángulos y polígonos en general, también de manera manipulativa.Se realiza un acercamiento a las relaciones métricas en un triángulo rectángulo: los teoremas del cateto y la altura.
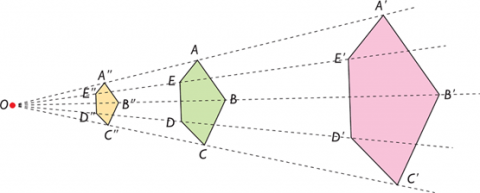
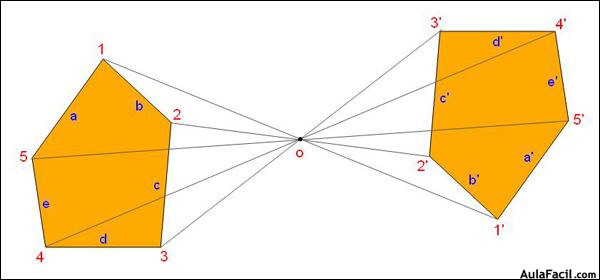
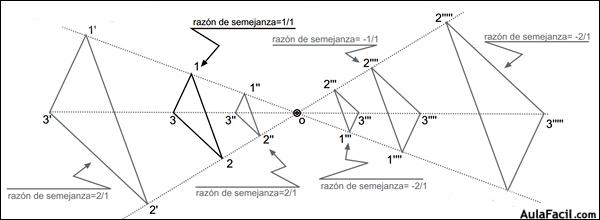
| CONOCE Se llama homotecia de centro O y razón k (distinto de cero) a la transformación que hace corresponder a un punto A otro A´, alineado con A y O, tal que: OA´=k·OA. Si k>0 se llama homotecia directa y si k<0 se llama homotecia inversa. |
| HOMOTECIA : | ||||||||
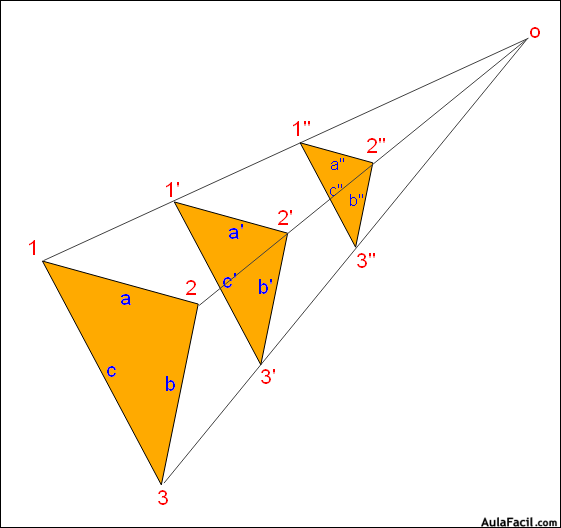
| La Homotecia es una transformación geométrica, una correspondencia entre dos figuras en la que se cumple que las parejas de puntos homotéticos están alineados con el centro de homotecia O y los segmentos homotéticos son paralelos. | ||||||||
| ||||||||
| Cuando los dos puntos homotéticos se encuentran al mismo lado respecto al centro, la homotecia es directa . | ||||||||
| Las figuras homotéticas directas son semejantes y nunca son equivalentes. | ||||||||
|
OBSERVA Y APRENDE
LEE Y APRENDE
COMO REALIZAR UNA HOMOTECIA
PRACTICA Y APRENDE