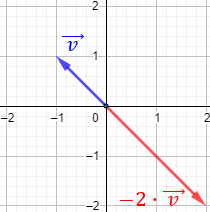
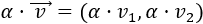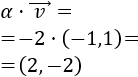Producto de un escalar por un vector de R²
Propiedades
- Si |α|> 1, el vector α·v tiene módulo mayor que v.
- Si |α|< 1, el vector α·v tiene módulo menor que v.
- Más exactamente,
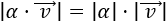
- Si α > 0, el vector α·v tiene el mismo sentido que v.
- Si α < 0, el vector α·v tiene sentido contrario que v.
- El producto es distributivo respecto de la suma de vectores:
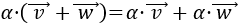
- El producto es distributivo respecto de la suma de escalares:
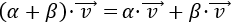
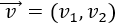 El producto del escalar α por el vector v es
El producto del escalar α por el vector v es