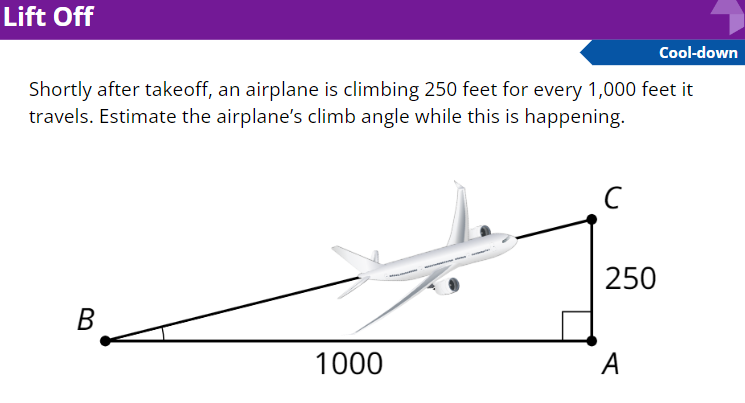
L4.4 - Ratios in Right Triangles
Learning Intentions and Success Criteria
We are learning to:
- Comprehend that knowing one acute angle of a right triangle determines all the ratios of side lengths in that triangle
- Generate ratios of side lengths of right triangles (using words and other representations)
- Build a table of ratios of side lengths of right triangles.
4.1: Ratio Rivalry
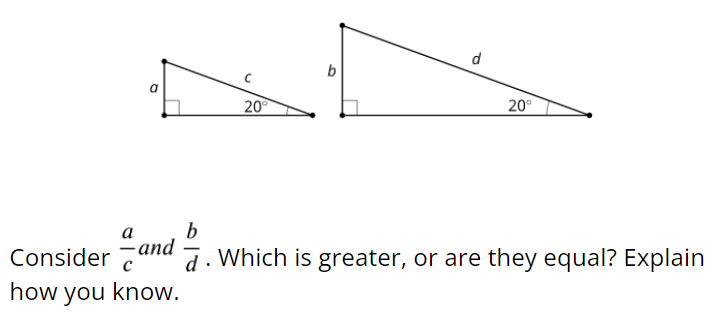
4.2: Tons of Triangles
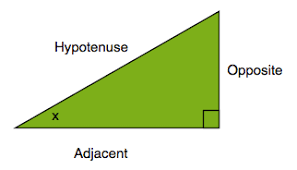
Open BOOK - Geo.4.4 Ratios in Right Triangles. Use the applet to explore right triangles.
1. & 2. Use the applet to build 4 different right triangles for each of your angles and record the side lengths of each of the triangles. Angle Adjacent Opposite Hypotenuse
3. Compute these 3 quotients for the acute angles in each triangle:
a. The length of the leg adjacent to your angle divided by the length of the hypotenuse
b. The length of the leg opposite from your angle divided by the length of the hypotenuse
c. The length of the leg opposite from your angle divided by the length of the leg adjacent to your angle

4. Find the mean of each type of quotient.

5. What do you notice? What do you wonder?
4.3: Tons of Ratios
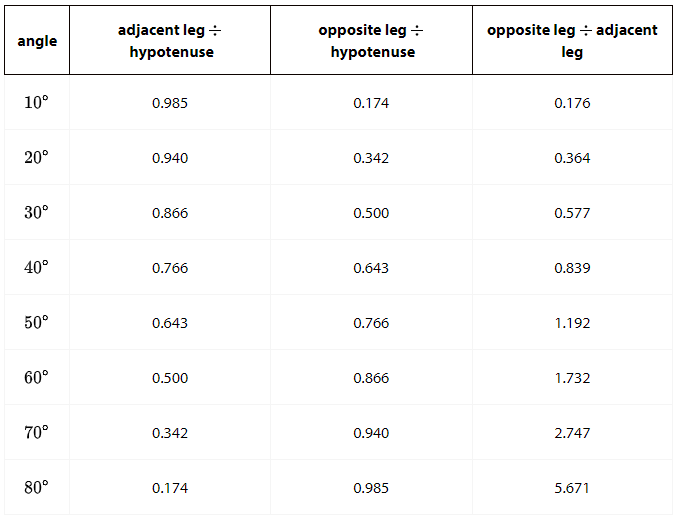
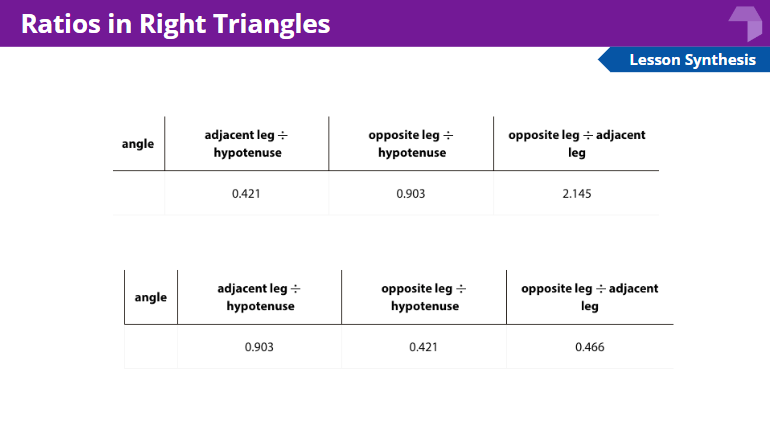
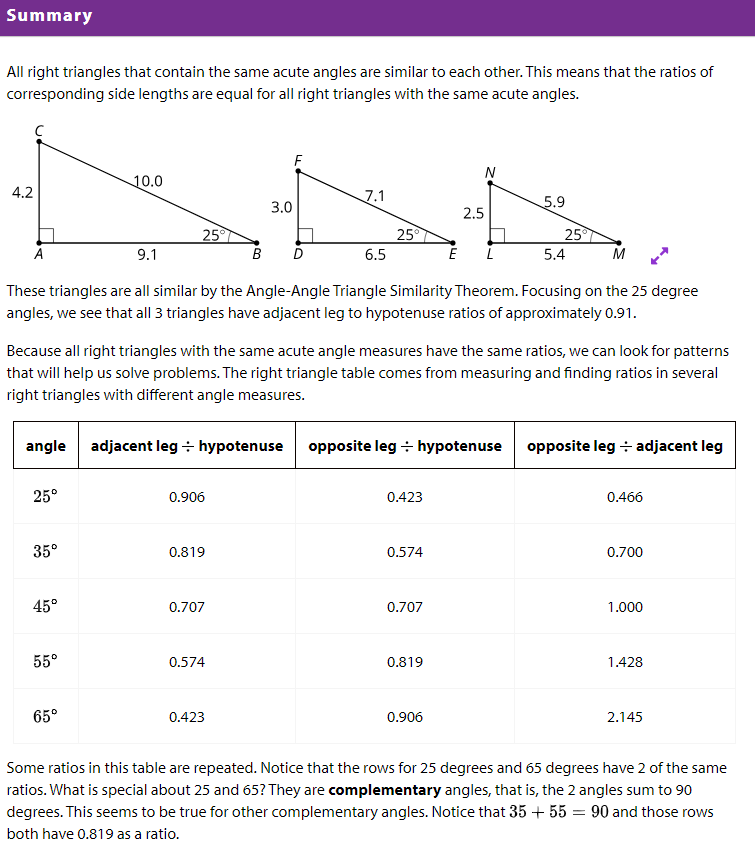
Students use the above right triangle table. 1. Compare the row for 20 degrees and the row for 70 degrees in the right triangle table. What is the same? What is different?

Complete the row for 35 degrees.
3. What do you know about a triangle with an adjacent leg to hypotenuse ratio value of 0.839?
Learning Intentions and Success Criteria
We are learning to:
- Comprehend that knowing one acute angle of a right triangle determines all the ratios of side lengths in that triangle
- Generate ratios of side lengths of right triangles (using words and other representations)
- Build a table of ratios of side lengths of right triangles.