Concepto de límite (de una función)
En esta página explicamos intuitivamente el concepto de límite de una función (de una variable: x), tanto en un punto finito como infinito.
1. Límite en un punto finito
Decimos que el límite de f(x) cuando x tiende al punto a es L si la función toma valores cada vez más cercanos a L cuando x toma valores cada vez más cercanos al punto a.
Lo expresamos mediante
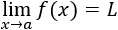 Ejemplo:
Consideremos la función f(x) = x2. Para calcular su límite en el punto x = 2, damos a x valores cercanos a 2 por su izquierda y su derecha.
Por la izquierda:
Ejemplo:
Consideremos la función f(x) = x2. Para calcular su límite en el punto x = 2, damos a x valores cercanos a 2 por su izquierda y su derecha.
Por la izquierda:
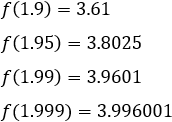 Por la derecha:
Por la derecha:
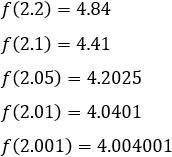 Se observa que la función tiende a 4 por ambos lados de 2. Por tanto, su límite es 4:
Se observa que la función tiende a 4 por ambos lados de 2. Por tanto, su límite es 4:
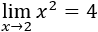 Gráfica de la función:
Gráfica de la función:
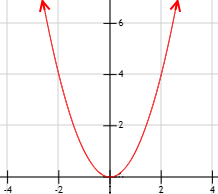 Si la función tiende a puntos distintos por uno y otro lado del punto a, entonces no existe el límite de la función en dicho punto.
Observad que, normalmente, el límite de f(x) en el punto a coincide con su imagen, es decir, con f(a) . Para ser más exactos, esto ocurre en las funciones que son continuas en el punto a.
Un ejemplo de función discontinua es f(x) = 1/x2 , cuyo límite cuando x tiende a 0 no coincide con f(0) porque la función ni siquiera está definida en dicho punto (no podemos dividir entre 0).
Si la función tiende a puntos distintos por uno y otro lado del punto a, entonces no existe el límite de la función en dicho punto.
Observad que, normalmente, el límite de f(x) en el punto a coincide con su imagen, es decir, con f(a) . Para ser más exactos, esto ocurre en las funciones que son continuas en el punto a.
Un ejemplo de función discontinua es f(x) = 1/x2 , cuyo límite cuando x tiende a 0 no coincide con f(0) porque la función ni siquiera está definida en dicho punto (no podemos dividir entre 0).
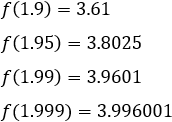 Por la derecha:
Por la derecha:
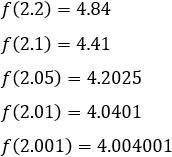 Se observa que la función tiende a 4 por ambos lados de 2. Por tanto, su límite es 4:
Se observa que la función tiende a 4 por ambos lados de 2. Por tanto, su límite es 4:
 Si la función tiende a puntos distintos por uno y otro lado del punto a, entonces no existe el límite de la función en dicho punto.
Observad que, normalmente, el límite de f(x) en el punto a coincide con su imagen, es decir, con f(a) . Para ser más exactos, esto ocurre en las funciones que son continuas en el punto a.
Un ejemplo de función discontinua es f(x) = 1/x2 , cuyo límite cuando x tiende a 0 no coincide con f(0) porque la función ni siquiera está definida en dicho punto (no podemos dividir entre 0).
Si la función tiende a puntos distintos por uno y otro lado del punto a, entonces no existe el límite de la función en dicho punto.
Observad que, normalmente, el límite de f(x) en el punto a coincide con su imagen, es decir, con f(a) . Para ser más exactos, esto ocurre en las funciones que son continuas en el punto a.
Un ejemplo de función discontinua es f(x) = 1/x2 , cuyo límite cuando x tiende a 0 no coincide con f(0) porque la función ni siquiera está definida en dicho punto (no podemos dividir entre 0).2. Límite en un punto infinito
Decimos que el límite de f(x) cuando x tiende a más infinito (+∞) es L si la función toma valores cada vez más cercanos a L cuando x crece indefinidamente.
Lo expresamos mediante
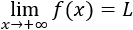 Análogamente, el límite de f(x) cuando x tiende a menos infinito (-∞) es L si la función toma valores cada vez más cercanos a L cuando x decrece indefinidamente.
Lo expresamos mediante
Análogamente, el límite de f(x) cuando x tiende a menos infinito (-∞) es L si la función toma valores cada vez más cercanos a L cuando x decrece indefinidamente.
Lo expresamos mediante
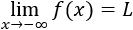 Ejemplos:
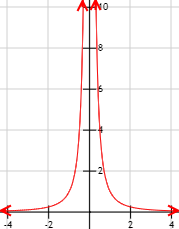
El límite es 0 porque un cociente positivo toma valores positivos más pequeños a medida que su denominador aumenta. Por tanto, cuando el denominador tiende a infinito, el cociente tiende a 0.
Gráfica de la función:
Ejemplos:
El límite es 0 porque un cociente positivo toma valores positivos más pequeños a medida que su denominador aumenta. Por tanto, cuando el denominador tiende a infinito, el cociente tiende a 0.
Gráfica de la función:

3. Más ejemplos
Límite 1
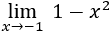 Los polinomios son funciones continuas, así que su límite en un punto finito a siempre es f(a).
Calculamos el límite sustituyendo el punto:
Los polinomios son funciones continuas, así que su límite en un punto finito a siempre es f(a).
Calculamos el límite sustituyendo el punto:
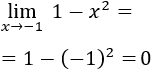 Gráfica de la función:
Gráfica de la función:
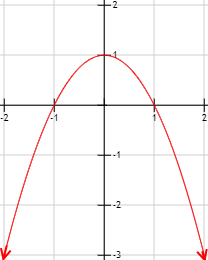 El límite de un polinomio cuando x tiende a infinito (positivo o negativo) siempre es infinito. El signo del infinito del límite depende el grado y del coeficiente principal del polinomio.
Límite 2
El límite de un polinomio cuando x tiende a infinito (positivo o negativo) siempre es infinito. El signo del infinito del límite depende el grado y del coeficiente principal del polinomio.
Límite 2
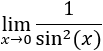 El seno de 0 es 0 y, por tanto, su cuadrado también es 0. Como un cuadrado es siempre no negativo, el denominador tiende a 0 por ambos lados.
Cuando el denominador de una fracción positiva decrece, el cociente crece. Por tanto, cuando x se acerca a 0, la función toma valores muy grandes. Es decir, el límite es infinito:
El seno de 0 es 0 y, por tanto, su cuadrado también es 0. Como un cuadrado es siempre no negativo, el denominador tiende a 0 por ambos lados.
Cuando el denominador de una fracción positiva decrece, el cociente crece. Por tanto, cuando x se acerca a 0, la función toma valores muy grandes. Es decir, el límite es infinito:
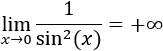 Gráfica de la función:
Gráfica de la función:
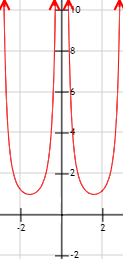
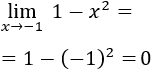 Gráfica de la función:
Gráfica de la función:
 El límite de un polinomio cuando x tiende a infinito (positivo o negativo) siempre es infinito. El signo del infinito del límite depende el grado y del coeficiente principal del polinomio.
Límite 2
El límite de un polinomio cuando x tiende a infinito (positivo o negativo) siempre es infinito. El signo del infinito del límite depende el grado y del coeficiente principal del polinomio.
Límite 2
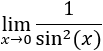 El seno de 0 es 0 y, por tanto, su cuadrado también es 0. Como un cuadrado es siempre no negativo, el denominador tiende a 0 por ambos lados.
Cuando el denominador de una fracción positiva decrece, el cociente crece. Por tanto, cuando x se acerca a 0, la función toma valores muy grandes. Es decir, el límite es infinito:
El seno de 0 es 0 y, por tanto, su cuadrado también es 0. Como un cuadrado es siempre no negativo, el denominador tiende a 0 por ambos lados.
Cuando el denominador de una fracción positiva decrece, el cociente crece. Por tanto, cuando x se acerca a 0, la función toma valores muy grandes. Es decir, el límite es infinito:
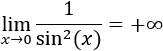 Gráfica de la función:
Gráfica de la función:
