メジャースケール上の和音
このワークシートはMath by Codeの一部です。
アプレット、背景、実装の順に見ていきましょう。

1.背景
音楽の背景は数学というよりも、
算数でたいていのことは十分わかります。
ただし、自然数すら0スタートで数える数学とはちがって、
1個目が1という素朴な数え方なので、かえって違和感があるかもしれません。
肩の力をぬいて、気楽に調べましょう。
<白鍵だけで長調と短調ができる>
音と音の間隔の基本は全音と半音です。
楽器の鍵盤を用意します。キーボードアプリでも、写真でもなんでもいいです。
白鍵が下にあり、黒鍵が挟まるところと白鍵が続くところがあります。
白鍵がとなりあう方がレアですね。
白鍵と白鍵の間に1つ黒鍵が入る音程(音の隔たり、インターバル)を全音、隣り合う鍵盤の音程を半音
といいました。
主音(スタート)を1として「ド」(C)から
白鍵だけを1、2、3、4、5、6、7、8と数えます。
これをドレミファソラシド (ハニホヘトイロハ=C,D,E,F,G,A,B,C)と呼びますね。
この音の階段、音階(スケール)をメジャー(長調)といいました。
だから、このドレミファソラシドの音階はハ長調(Cメジャー)スケールと言えますね。
だから、黒鍵のありを2、なしを1とすると、2212221の音程ですから、全全半全全全半です。
主音(スタート)を1として「ラ」(A)から
白鍵だけを1,2,3,4,5,6,7,8と数えます。
これをラシドレミファソラ(イロハニホヘト=ABCDEFGA)と呼びますね。
この音のスケールをマイナー(短調)といいました。
だから、このラシドレミファソラの音階をイ短調(Aマイナー)スケールと言えますね。
黒鍵のありなしで21221222で、全半全全半全全全になっています。
数字だけ見ると、とても不規則で嫌な感じがする人もいるでしょう。
たとえば、ヤマハのPSS-A50は1周期12鍵盤×3+1=37鍵盤あります。
鍵盤の最低の音ド(C2)から、最高の音ド(C5)まであります。
番号が12増えると音程が1オクターブ上がり、音名は変わらないですね。
<白鍵だけでスケールが増やせる>
白鍵だけひくときに、Cを1にするとメジャー、Aを1にするとマイナーでした。
では、他の白鍵をスタートの1にすると音程と音階はどうなるでしょう。
実は大昔からわかっていて、教会モードという音階名まで1つ1つついています。
C=1はイオニアン(メジャー)全全半全 全全半
D=1はドリアン 全半全全 全半全
E =1はフリジアン 半全全全 半全全
F =1はリディアン 全全全半 全全半
G=1はミクソ・リディアン 全全半全 全半全
A=1はエオリアン 全半全全 半全全
B=1はロクリアン 半全全半 全全全
名前の由来と使い方とかは今は、気にしないことにします。
音程を「ただの文字列」として観察してみましょう。
質問:7つの教会モードのスケールの共通点とちがいを探ろう。
音階の1個目の白鍵を、ただ、C,D,E,F,G,A,Bと1つ右にずらしていっただけでした。
だから、音程の全全半全全全半も1こずつ進んでいますね。
「全全半全全全半」を文字列としてみると、始まりが違うだけで、並びの周期は同じです。
さらに、面白いのは、最初の4文字はB=1のロクリアンを除いて、全3個と半1個があります。
だから、1番と5番の音程は全×3+半で共通になっています。これを完全5度といいます。
完全5度はすごいですね。
CならG、DならA、EならB、
FならC、GならD、AならE
これらはほぼほぼどんなスケールでも綺麗に聞こえるということです。
完全5度は、また、和音(コード)を時間とともにつないでいく、コード進行の上でも大切です。
キーボードでいうと、白黒が交互に並ぶのに1つだけ白白をはさむ5番目です。
(ロクリアンモードだけは半全全半だから、1つの全が半になっていて音程が短いね。
だから、このレアな5度を減5度(-5)といいます。)
<他の完全は?>
完全5度が1つの例外を除いて、普遍的にみられることがわかりました。
では、他の完全な音程を探してみましょう。
あります。
1番から8番までいくと、かならず1オクターブ上がるので完全8度という名前がついています。
当たりまえでつまらないです。
あります。
1番から4番までいくと、全全半、全半全、半全全のどれかになる。(例外はリディアンの全全全)
この全+全+半のことを、完全4度といます。
キーボードでは白鍵の4番目までに白白が1つはさむ音程です。
CならF、DならG、EならA、
GならC、AならD、BならE
完全4度の音を選ぶと、綺麗に聞こえるということですね。
また、完全4度は、コード進行でも大切です。
<ダイアトニック3和音>
2,3,4をとばして、白鍵の1番と5番を同時に押してみます。
完全5度を重ねておけば、メジャーもマナー区別のない2和音ができます。
では3度を重なるとどうなるでしょうか。
2、4を飛ばして、白鍵の1番と3番と5番を同時に押してみます。
C=1はイオニアン(メジャー)全全半全全全半
D=1はドリアン 全半全全全半全
E =1はフリジアン 半全全全半全全
F =1はリディアン 全全全半全全半
G=1はミクソ・リディアン 全全半全全半全
A=1はエオリアン 全半全全半全全
B=1はロクリアン 半全全半全全全
半半というのはありえないので、全全か全半か半全です。
全全というのは長3度(メジャー3)、全半か半全が短3度(マイナー3)です。
1つとばしで、白鍵の奇数番号、1,3,5を同時に引いたのが3和音です。
C=1の1,3,5はC3、つまり、C
D=1の1,3,5はD-3、つまり、Dm
E=1の1,3,5はE-3、つまり、Em
F=1の1,3,5はF3、つまり、F
G=1の1,3,5はG3、つまり、G
A=1の1,3,5はA-3、つまり、Am
B=1の1,3,5はB-3・-5、つまり、Bm-5
この和音は、Cメジャースケールの音だけを使った和音なので、
特別な名前、ダイヤトニックスケールコードという名前がついてます。
もし、Cメジャースケール(C,D,E,F,G,A,B)ならコードは、
1,4,5番(度)のC,F,Gはメジャーです。
のこり、1,4番(度)の間D,Eと5、8番(度)の間A,Bはマイナーです。特に7番(度)は
m-7という独特に不安定な響きのコードになります。
ここで、絶対的にスケールの1に合わせた、度数で再表示してみましょう。
そして、7を超えた分は7をひき、小さい度数(番号)順に表示します。(つまり、疑似mod7)
1,3,5はC
2,4,6はDm
3,5,7はEm
1,4,6はF
2,5,7はG
1,3,6はAm
2,4,7はBm-5
ダイアトニックスケールコードは7つありますが、1つおきに見ると、
白鍵の番号が2つずれるだけなので、2音ずつ共通音があります。コード名を音の集合ととらえると、
積集合の要素が2個ということです。
C∩Em={3,5}
Dm∩F={4,6}
Em∩G={5,7}
F∩Am={1,6}
G∩Bm-5={2,7}
Am∩C={1,3}
Bm-5∩Dm={2,4}
Cから見るとEmとAmは2音共通なので類似度が高いですね。
Fから見るとDmとAmは近いです。
Gから見るとEmとBm-5は近いです。
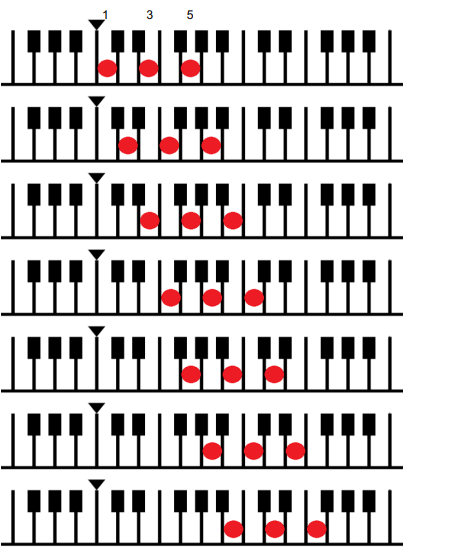
<ダイアトニック4和音>
2,4,6を飛ばして、白鍵の1番と3番と5番と7番を同時に押してみます。
C=1はイオニアン(メジャー)全全半全全全半
D=1はドリアン 全半全全全半全
E =1はフリジアン 半全全全半全全
F =1はリディアン 全全全半全全半
G=1はミクソ・リディアン 全全半全全半全
A=1はエオリアン 全半全全半全全
B=1はロクリアン 半全全半全全全
1番から7番までの音程は全5半1か全4半2のどちらかです。
半1というのは長7度(メジャー7)、半2が短7度(マイナー7)ですが、
マイナー7が普通なのでマイナーをつけずにただの7度といいます。
1つとばしで、白鍵の奇数番号、1,3,5を同時に引いたのが3和音です。
C=1の1,3,5、7はC3・7、つまり、Cmaj7
D=1の1,3,5、7はDー3・ー7、つまり、Dm7
E=1の1,3,5、7はEー3・ー7、つまり、Em7
F=1の1,3,5、7はF3・7、つまり、Fmaj7
G=1の1,3,5、7はG3・ー7、つまり、G7
A=1の1,3,5、7はA-3・-7、Am7
B=1の1,3,5、7はB-3・-5・-7、つまり、Bm7-5
ここで、絶対的にスケールの1に合わせた、度数で再表示してみましょう。
そして、7を超えた分は7をひき、小さい度数(番号)順に表示します。(つまり、疑似mod7)
1,3,5、7はCmaj7
1、2,4,6はDm7
2、3,5,7はEm7
1,3、4,6はFmaj7
2,4、5,7はG7
1,3,5、6はAm7
2,4,6、7はBm7-5
ダイアトニックスケールコードは7つありますが、1つおきに見ると、
白鍵の番号が2つずれるだけなので、3音ずつ共通音があります。
コード名を音の集合ととらえると、積集合の要素が3個ということです。
(例)Am7 ∩ C={1,3,5}
C={1,3,5}(1番とする)からみてEm7(3番m7)、Am7(6番m7)が近いです。
F={4,6,1}(4番)からみてDm7(2番m7)、Am7が近いです。
G={2,5,7}(5番)からみてEm7、Bm7-5(7番m7-5)が近いです。
ただし、キーとなる1番目の和音をトニックといい、主たる響きになります。
だから、1つおきの類似性という視点から見たら、1つおきに代理コードとして使えそうですが、
瞬間瞬間の響きの共通点だけではなく、通したときの視点からみると、トニックの代理が最優先になります。
1番の代理は3m7、6m7の2個 覚え方1±2=3m、-1m≡3m7、6m7
4番の代理は2m7の1個 覚え方4-2=2m
5番の代理は7m7-5の1個 覚え方5+2=7m7-5
が標準的な考え方になるようです。
<楽器演奏の場面では>
たとえば、ピアノでは、左手でベース音(コードの1の音)を鳴らしたり、
合奏では、ベース担当の人がいたりします。
だから、セブンスの音を出すときは、
・ベース音を半音下げたのがmaj7
・ベース音を全音下げたのが7
という解釈をすることが多いです。それは、ギター演奏でもそうです。
ベースランニングという奏法まであるくらいです。
そもそも、ベース音とセブンス音は順に押さえると開きすきて大変。
オクターブを上げ下げすると、ベースとセブンスは音が近くて衝突しやすい。
だから、ベースをぬいてしまうのですね。

2、実装
質問:12個の主音に対するメジャースケール上の7つのコードを表示するアプレットを作るにはどうしたらよいでしょう。
クロマチック音名を文字列にします。
NameS={"B","C","C#","D","D#","E","F","F#","G","G#","A","A#"} //音名の#系です。
C4={"maj7","m7","m7","maj7","7","m7","m7-5"} //4和音
C3={"","m","m","","","m","m-5"} //3和音
名前リストを2オクターブ分とります。
NS2=join(NameS,NameS)
インデックスはgeogebraなら1から24番になります。
たとえば、Bを主音にしたときにメジャースケールのインデックスは
M={1,3,5、6、8,10,12}ですから、
k=NameS2(n)を主音にするメジャースケールのドレミファソラシド名は
doremi=sequence(NS2(k-1+M(i)), i, 1,7)
doremi+C3で3和音、
doremi+C4で4和音の和音名になります。
キーを選ぶスライダーをn(1以上12以下)とすると、
選んだキーはNameS(n)のテキストになります。
(コードやキーの名前を♭にした表示も考えましたが、内部バグらしく、表示がちがってました。)
このアプレットは、キーを指定すると、
そのキーのスケールでの和音名が出るのは便利ですが、コードの音程の理由は確認できません。
質問:スケールの音程とコードの音程が視覚化できるアプレットはどうやって作りますか?
12種類の音名があるので、12角形の点にします。
たとえば、e^(i 2π/k) k=1...12として、12個の複素数z1からz12を設定しましょう。
12音名のリストNameS={"B", "C",......., "A#"}にたいして、
NameS(1), NameS(2),....,NameS(12)を1つ1つのテキストオブジェクトとして、
txt1, txt2,.....txt12と名前をつけなおします。
そうして、それぞれのテキストオブジェクトtxt kの「設定」の「位置」のリストから対応するzk
を選ぶべば、12個の頂点に、音名を表示できるようになるでしょう。
1つ1つの複素数の他に、複素数のリストpt=sequence(e^(i 2π/k), k, 1, 12)を設定しておけば、
pt(x)のxを適当に選ぶことで、スケールに関係のある点を強調できます。
(そして、選ばれた番号の頂点kに対して、mod(k-1,12)+1をすることで、12のときに12にする
変則mod12を作ることで、kの変化に対して、1,2、…、12、1,2、…。12と返します。)
選ばれたスケールの番号M={1,3,5、6、8,10,12}
キーをn=2としたばあい、M+n-1={2, 4, 6, 7, 9,11,13}と、リストをシフトして、MNという名前をつけます。そして、Sequence(Mod(MN(k)-1, 12)+1,k,1,7)とすると、12をこえたら12けずれます。
それをMN2とすると={ 2, 4, 6, 7, 9,11,1}となり、複素数の番号をはずしてた分を、12個に納めます。
ここで、zip(pt(k),k,MN2)とするとMN2番目の頂点、つまりキーが2のスケール音名を強調できますね。
最後に和音がサイクリックな音名の関係、つまり円環構造なので、
スケール上の3和音、4和音の点を多角形の頂点として選びだしましょう。
3和音ならば、その和音がキーのi 番目なら、Cp3={MN2(i),MN2(i+2),MN2(i+4)}と番号リストを作ります。すると、12等分の点からpolygon(pt(Cp3(1)),pt(Cp3(2)),pt(Cp3(3)))
とするだけで三角形が指定できます。
4和音場合は、スケール上の位置MN2で、さらに偶数番増やせばよいですね。
くわしくは、かくれた「数式」を広げて、グラフィックビューを一時的にせまくして、観察しましょう。