Algebraický důkaz
Věta
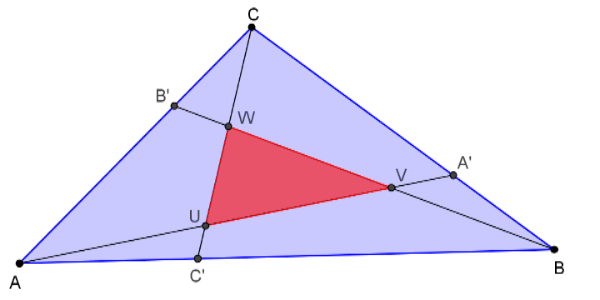
Mějme libovolný trojúhelník v rovině. Jestliže každý jeho vrchol spojíme s bodem, který leží v jedné třetině protilehlé strany, pak trojúhelník tvořený těmito spojnicemi má obsah o velikosti jedné sedminy obsahu původního trojúhelníku.
Algebraický důkaz (dle Feynmana)
Nechť trojúhelník ABC je rovnostranný a platí, že AB = BC = AC = 3. Pak C'B = 1. Dle kosinové věty platí CC'2=32+1-6 cos 60°=7. Trojúhelníky CBC' a BUC' jsou podobné dle věty uuu, protože mají jeden společný úhel (UC'B = BC'C) a zároveň úhly UBC' = BCC'. Pak tedy
Ze symetrie pak vyplývá, že UVW je také rovnostranný trojúhelník se stranami o délce délky stran trojúhelníku ABC. Proto SUVW=SABC.