Funzioni
Definizione e lessico sulle funzioni matematiche
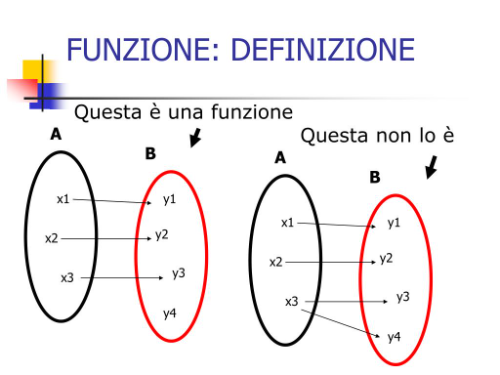
Dato un insieme di partenza e un insieme di arrivo, si definisce funzione una relazione matematica che ad ogni elemento dell'insieme associa un solo elemento dell'insieme .
L'insieme di tutti gli elementi di per cui è definita la funzione, si chiama dominio della funzione.
Il sottoinsieme di di tutti gli elementi che assume la funzione si chiama codominio o insieme immagine o insieme delle immagini.
I gli elementi del codominio, ovvero i valori assunti dalla funzione, si chiamano immagini. Per ogni immagine, il valore di partenza si chiama controimmagine.
Funzione iniettiva
Una funzione si dice iniettiva, se per ogni immagine esiste una e una sola controimmagine.
Sul piano cartesiano, se ogni retta orizzontale tracciata sul grafico NON ammette più di una intersezione con il grafico della funzione.
Funzione suriettiva
Una funzione si per ogni elemento dell'insieme di arrivo esiste almeno una controimmagine o, in altre parole, se l'insieme delle immagini coincide con l'insieme di arrivo.
Sul piano cartesiano, se l'insieme di arrivo è R, se ogni retta orizzontale ammette almeno un punto di intersezione con il grafico della funzione.
Funzione biiettiva
Se una funzione è sia iniettiva che suriettiva, allora si dice che la funzione è biiettiva.