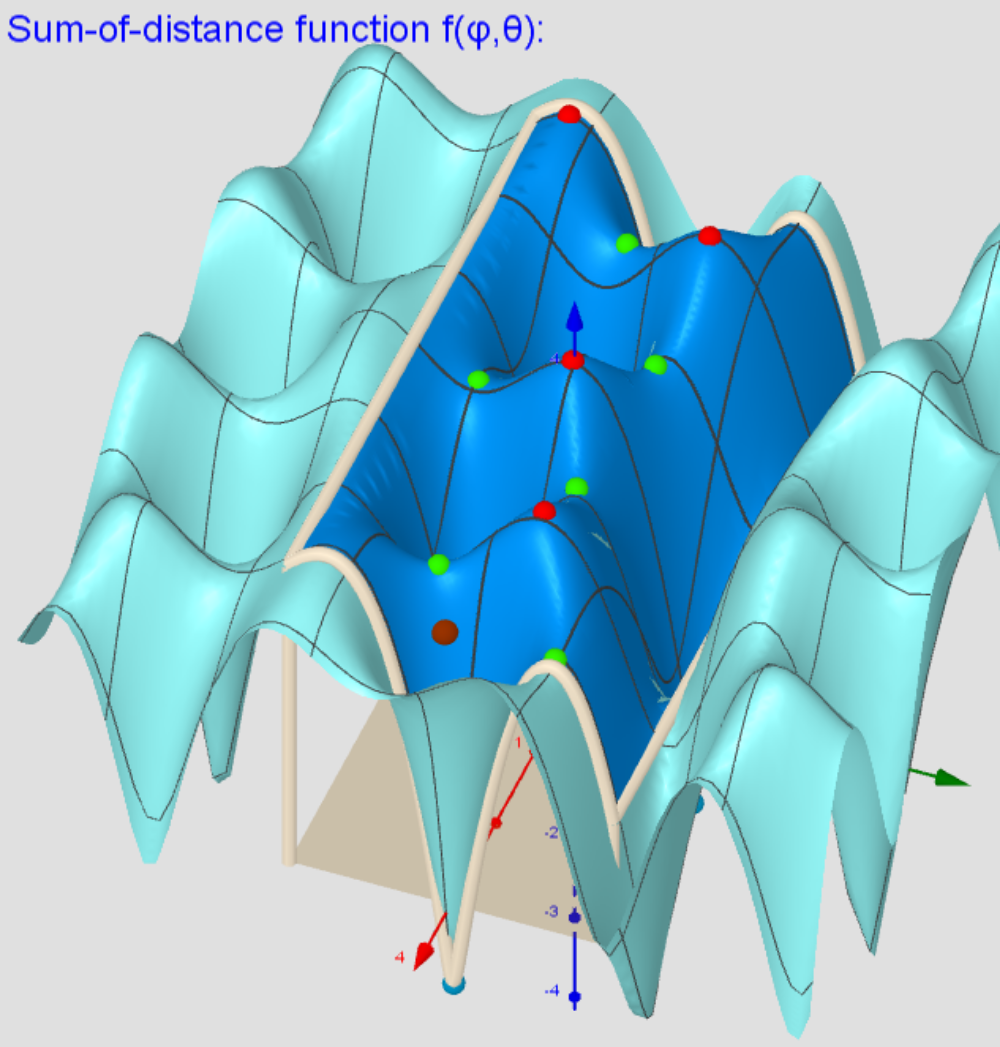
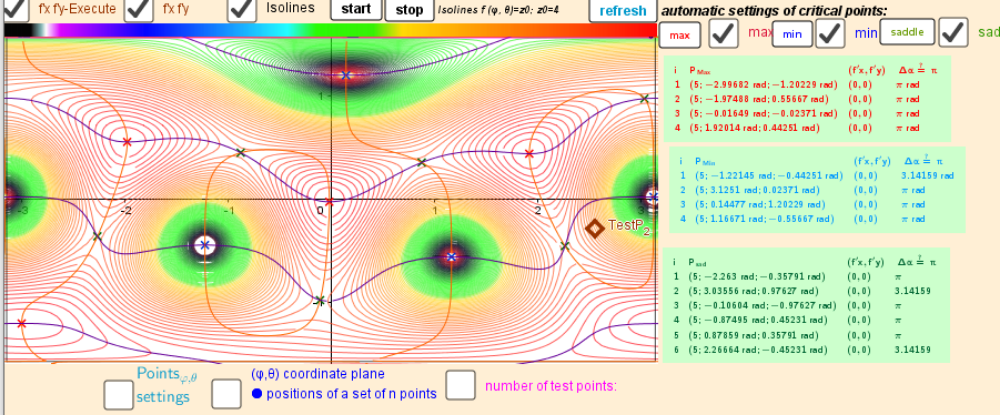
n=4 Tetrahedron. Images: A critical points scheme for Generating uniformly distributed points on a sphere.
The applet illustrates the case where 4 vertices of a regular tetrahedron "induce" the vertices of two other polyhedra:
4 ●Regular Tetrahedron← 4 ●Regular Tetrahedron →6 ●Regular Octahedron.
Description are in https://www.geogebra.org/m/y8dnkeuu and https://www.geogebra.org/m/rkpxwceh.
![[size=50]A system of points on a sphere S of radius R “induces” on the sphere S0 of radius R0 three different sets of points, which are [color=#93c47d]geometric medians (GM)[/color] -local [color=#ff0000]maxima[/color], [color=#6d9eeb]minima[/color] and [color=#38761d]saddle[/color] points sum of distance function f(x). The angular coordinates of the spherical distribution of a system of points -[color=#0000ff] local minima[/color] coincide with the original system of points.[/size]](https://stage.geogebra.org/resource/bgkr6g9c/O7mWkgBjcRAcDbh5/material-bgkr6g9c.png)
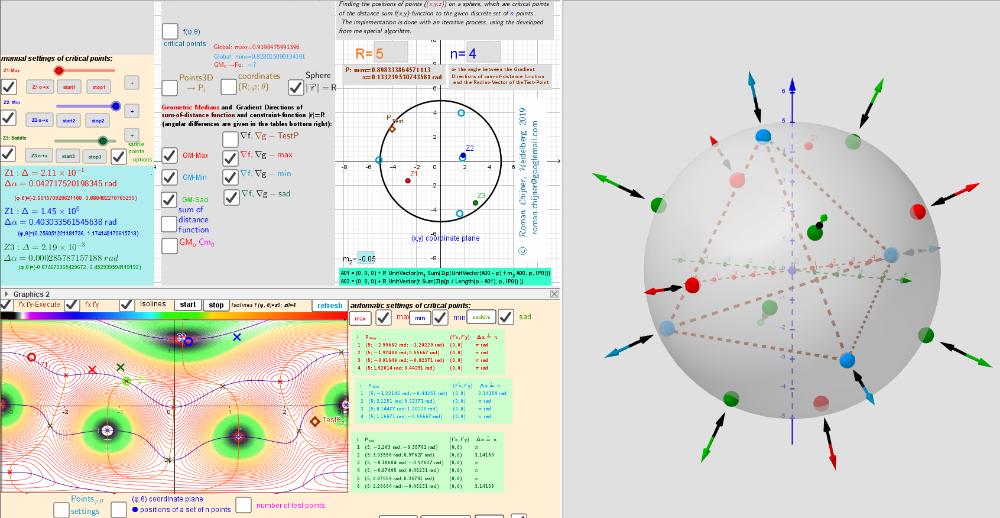
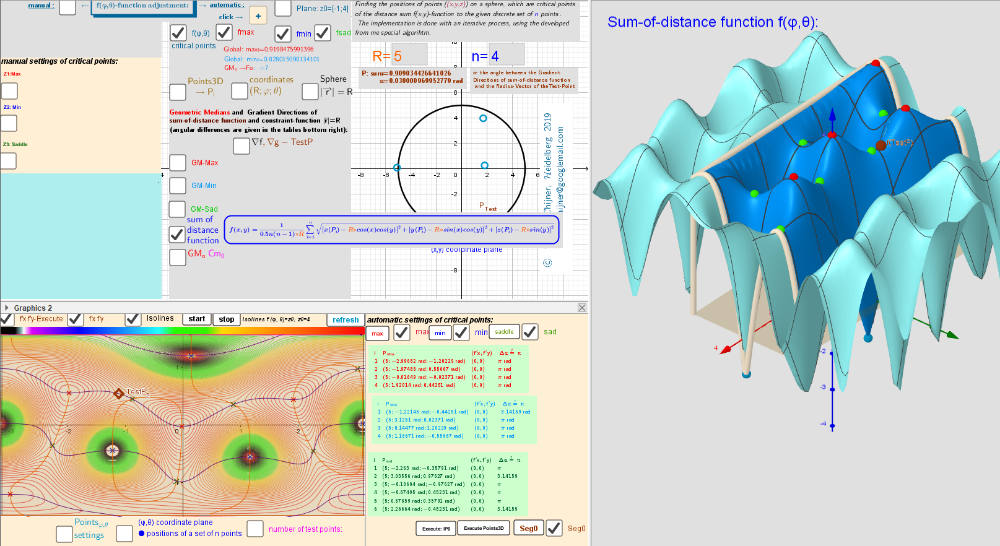
![Distribution of points Pi, [color=#5b0f00]test Point[/color], [color=#ff0000]Max[/color]/[color=#0000ff]min[/color]/[color=#38761d]saddle[/color] -[color=#333333]Critical points[/color] on a sphere. Vectors ∇f and ∇g at these points.](https://stage.geogebra.org/resource/xuk2mxys/SANXm4VKGncY22eU/material-xuk2mxys.png)
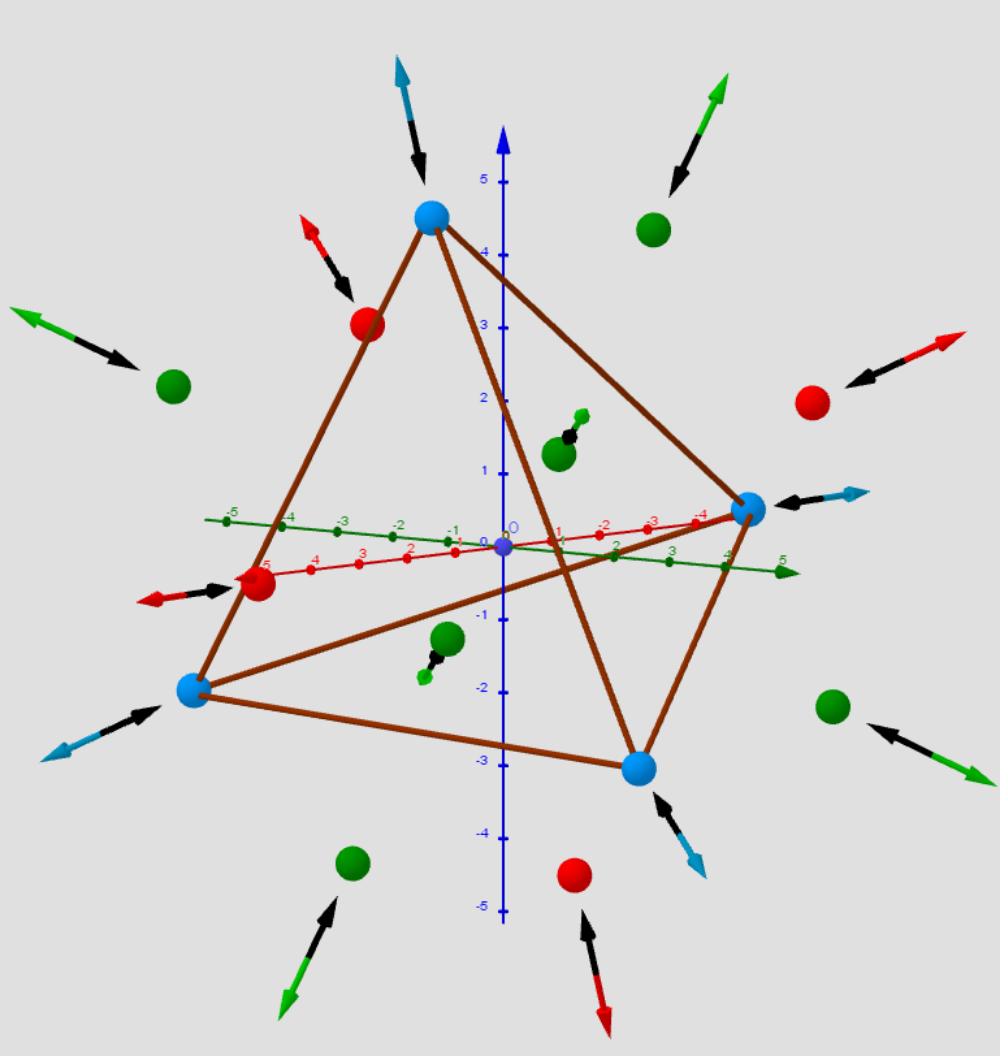
![[color=#ff0000]max:[/color] Tetrahedron [color=#0000ff]min: [/color]Tetrahedron [color=#6aa84f]sad:[/color] Octahedron](https://stage.geogebra.org/resource/dt8amswa/2AVQIEyXxNyvquhr/material-dt8amswa.png)