Sobras de vidro
Numa vidraria existem sobras de vidro na forma de triângulos retângulos isósceles, cujos catetos têm 30 cm de comprimento.
Pretende-se fazer o aproveitamento destas sobras e, para isso, o administrador solicitou a dois funcionários que fizessem um estudo de modo a obter retângulos com a maior área possível.
Constrói no applet seguinte a figura dinâmica estudada pelo António:
1.º O triângulo retângulo isósceles cujos catetos medem 30 cm;
2.º Um ponto P que se desloca no lado BC;
3.º Um retângulo como esquematizado na figura:
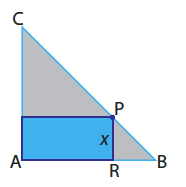
Desloca o ponto P e regista a variação do perímetro dos diferentes retângulos.
E como varia a área dos mesmos retângulos? Será que existe um retângulo de área máxima?
O Valdemar fez de forma diferente, considerou um ponto L pertencente ao lado AC e a partir
dele efetuou cortes paralelo e perpendiculares à hipotenusa, obtendo assim um retângulo como o da figura:
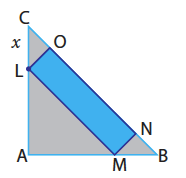
Constrói a figura dinâmica estudada pelo Valdemar:
O que acontece à variação do perímetro destes retângulos?
Quais são as dimensões do retângulo LMNO de modo que a área de vidro aproveitada seja máxima?
Qual dos dois cortadores de vidro está a gerar menos desperdício?