APOLLONIOS Problem
Apollonios' Problem lösen mit geogebra-Werkzeugen
Das Problem des APOLLONIOS von Perge (ca. 265 v. Chr. bis 190 v. Chr.) stellt die Aufgabe:
 gebra-Materialien findet man zahlreiche Aktivitäten zu diesem Problem, manches muss man unter dem Stichwort "Appolonius" suchen!
Im Applet oben werden 3 Kreise vorgegeben, als Grenzlage sind auch Punkte als Kreis mit Radius möglich. Dies genügt; denn eigentlich ist die Fragestellung eine Fragestellung der MÖBIUS-Geometrie.
Man sollte die Aufgabe auf der Kugel untersuchen: KREISE sind Ebenen-Schnitte mit der Kugel, für PUNKTE ist das ein Schnitt mit einer Tangentialebene. Die Unterscheidung Kreis - Gerade ist auf der Kugel unnötig.
Zu drei vorgegebenen KREISEN auf der Kugel gibt es bis zu 8 berührende KREISE. Da findet sich sicher ein Projektionszentrum auf der Kugel, so dass nach der stereographischen Projektion auf eine Ebene von diesem Zentrum aus alle beteiligten KREISE in der Ebene tatsächlich Kreise (oder Punkte) sind (dazu die nachfolgende Seite).
Wenn im Applet 2 der Kreise sich schon fast berühren, erzwingt ein "Klick" den Berührfall!
Lösungen mit ge
gebra-Materialien findet man zahlreiche Aktivitäten zu diesem Problem, manches muss man unter dem Stichwort "Appolonius" suchen!
Im Applet oben werden 3 Kreise vorgegeben, als Grenzlage sind auch Punkte als Kreis mit Radius möglich. Dies genügt; denn eigentlich ist die Fragestellung eine Fragestellung der MÖBIUS-Geometrie.
Man sollte die Aufgabe auf der Kugel untersuchen: KREISE sind Ebenen-Schnitte mit der Kugel, für PUNKTE ist das ein Schnitt mit einer Tangentialebene. Die Unterscheidung Kreis - Gerade ist auf der Kugel unnötig.
Zu drei vorgegebenen KREISEN auf der Kugel gibt es bis zu 8 berührende KREISE. Da findet sich sicher ein Projektionszentrum auf der Kugel, so dass nach der stereographischen Projektion auf eine Ebene von diesem Zentrum aus alle beteiligten KREISE in der Ebene tatsächlich Kreise (oder Punkte) sind (dazu die nachfolgende Seite).
Wenn im Applet 2 der Kreise sich schon fast berühren, erzwingt ein "Klick" den Berührfall!
Lösungen mit ge gebra-Werkzeugen
Diese Lösungsmöglichkeiten sind sicher nicht im Sinne der "reinen Lehre", welche die Hilfsmittel auf
gebra-Werkzeugen
Diese Lösungsmöglichkeiten sind sicher nicht im Sinne der "reinen Lehre", welche die Hilfsmittel auf 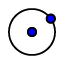 und
und 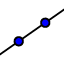 beschränken will; wir meinen jedoch, dass man auch auf diesem Wege etwas über solche Probleme erfahren kann. Beweise können sowieso auf diese Weise nicht (?) erbracht werden! Interessant ist auch die Frage, welche der ge
beschränken will; wir meinen jedoch, dass man auch auf diesem Wege etwas über solche Probleme erfahren kann. Beweise können sowieso auf diese Weise nicht (?) erbracht werden! Interessant ist auch die Frage, welche der ge gebra-Hilfsmittel sich durch Zirkel und Lineal ersetzen ließen.
Auf den vorangegangenen Seiten des ge
gebra-Hilfsmittel sich durch Zirkel und Lineal ersetzen ließen.
Auf den vorangegangenen Seiten des ge gebra-books haben wir illustriert, dass Mittellinien zweier Kreise zwei konfokale Kegelschnitte (
gebra-books haben wir illustriert, dass Mittellinien zweier Kreise zwei konfokale Kegelschnitte (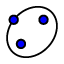 oder
oder 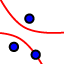 ) sind mit den Kreismittelpunkten
) sind mit den Kreismittelpunkten  als Brennpunkten. Sie sind die Ortslinien
als Brennpunkten. Sie sind die Ortslinien 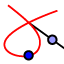 der Punkte, die von beiden Kreisen denselben Abstand besitzen.
Dies kann man auch so lesen: die Mittellinien sind die Ortslinien der Mittelpunkte von Kreisen, die die vorgegebenen Kreise berühren.
Zu drei Kreisen gibt es drei Kegelschnittpaare für die Mittelpunkte der Kreise, die jeweils zwei der vorgegebenen Kreise berühren.
Zwei Kegelschnitte schneiden
der Punkte, die von beiden Kreisen denselben Abstand besitzen.
Dies kann man auch so lesen: die Mittellinien sind die Ortslinien der Mittelpunkte von Kreisen, die die vorgegebenen Kreise berühren.
Zu drei Kreisen gibt es drei Kegelschnittpaare für die Mittelpunkte der Kreise, die jeweils zwei der vorgegebenen Kreise berühren.
Zwei Kegelschnitte schneiden  sich in bis zu 4 Punkten. Die Kegelschnitte von zwei der Kegelschnitt-Paaren schneiden sich in bis zu 16 Punkten.
Unter diesen Punkten gibt es bis zu 8 gemeinsame Schnittpunkte
sich in bis zu 4 Punkten. Die Kegelschnitte von zwei der Kegelschnitt-Paaren schneiden sich in bis zu 16 Punkten.
Unter diesen Punkten gibt es bis zu 8 gemeinsame Schnittpunkte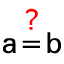 : dies sind die Mittelpunkte der gesuchten Berührkreise.
Unser Vorgehen für die "Konstruktion":
: dies sind die Mittelpunkte der gesuchten Berührkreise.
Unser Vorgehen für die "Konstruktion":
- konstruiere mit Zirkel
 und Lineal
und Lineal  zu drei vorgegebenen Kreisen (die) berührende(n) Kreise
zu drei vorgegebenen Kreisen (die) berührende(n) Kreise
 gebra-Materialien findet man zahlreiche Aktivitäten zu diesem Problem, manches muss man unter dem Stichwort "Appolonius" suchen!
Im Applet oben werden 3 Kreise vorgegeben, als Grenzlage sind auch Punkte als Kreis mit Radius möglich. Dies genügt; denn eigentlich ist die Fragestellung eine Fragestellung der MÖBIUS-Geometrie.
Man sollte die Aufgabe auf der Kugel untersuchen: KREISE sind Ebenen-Schnitte mit der Kugel, für PUNKTE ist das ein Schnitt mit einer Tangentialebene. Die Unterscheidung Kreis - Gerade ist auf der Kugel unnötig.
Zu drei vorgegebenen KREISEN auf der Kugel gibt es bis zu 8 berührende KREISE. Da findet sich sicher ein Projektionszentrum auf der Kugel, so dass nach der stereographischen Projektion auf eine Ebene von diesem Zentrum aus alle beteiligten KREISE in der Ebene tatsächlich Kreise (oder Punkte) sind (dazu die nachfolgende Seite).
Wenn im Applet 2 der Kreise sich schon fast berühren, erzwingt ein "Klick" den Berührfall!
Lösungen mit ge
gebra-Materialien findet man zahlreiche Aktivitäten zu diesem Problem, manches muss man unter dem Stichwort "Appolonius" suchen!
Im Applet oben werden 3 Kreise vorgegeben, als Grenzlage sind auch Punkte als Kreis mit Radius möglich. Dies genügt; denn eigentlich ist die Fragestellung eine Fragestellung der MÖBIUS-Geometrie.
Man sollte die Aufgabe auf der Kugel untersuchen: KREISE sind Ebenen-Schnitte mit der Kugel, für PUNKTE ist das ein Schnitt mit einer Tangentialebene. Die Unterscheidung Kreis - Gerade ist auf der Kugel unnötig.
Zu drei vorgegebenen KREISEN auf der Kugel gibt es bis zu 8 berührende KREISE. Da findet sich sicher ein Projektionszentrum auf der Kugel, so dass nach der stereographischen Projektion auf eine Ebene von diesem Zentrum aus alle beteiligten KREISE in der Ebene tatsächlich Kreise (oder Punkte) sind (dazu die nachfolgende Seite).
Wenn im Applet 2 der Kreise sich schon fast berühren, erzwingt ein "Klick" den Berührfall!
Lösungen mit ge gebra-Werkzeugen
Diese Lösungsmöglichkeiten sind sicher nicht im Sinne der "reinen Lehre", welche die Hilfsmittel auf
gebra-Werkzeugen
Diese Lösungsmöglichkeiten sind sicher nicht im Sinne der "reinen Lehre", welche die Hilfsmittel auf  und
und  beschränken will; wir meinen jedoch, dass man auch auf diesem Wege etwas über solche Probleme erfahren kann. Beweise können sowieso auf diese Weise nicht (?) erbracht werden! Interessant ist auch die Frage, welche der ge
beschränken will; wir meinen jedoch, dass man auch auf diesem Wege etwas über solche Probleme erfahren kann. Beweise können sowieso auf diese Weise nicht (?) erbracht werden! Interessant ist auch die Frage, welche der ge gebra-Hilfsmittel sich durch Zirkel und Lineal ersetzen ließen.
Auf den vorangegangenen Seiten des ge
gebra-Hilfsmittel sich durch Zirkel und Lineal ersetzen ließen.
Auf den vorangegangenen Seiten des ge gebra-books haben wir illustriert, dass Mittellinien zweier Kreise zwei konfokale Kegelschnitte (
gebra-books haben wir illustriert, dass Mittellinien zweier Kreise zwei konfokale Kegelschnitte ( oder
oder  ) sind mit den Kreismittelpunkten
) sind mit den Kreismittelpunkten  als Brennpunkten. Sie sind die Ortslinien
als Brennpunkten. Sie sind die Ortslinien  der Punkte, die von beiden Kreisen denselben Abstand besitzen.
Dies kann man auch so lesen: die Mittellinien sind die Ortslinien der Mittelpunkte von Kreisen, die die vorgegebenen Kreise berühren.
Zu drei Kreisen gibt es drei Kegelschnittpaare für die Mittelpunkte der Kreise, die jeweils zwei der vorgegebenen Kreise berühren.
Zwei Kegelschnitte schneiden
der Punkte, die von beiden Kreisen denselben Abstand besitzen.
Dies kann man auch so lesen: die Mittellinien sind die Ortslinien der Mittelpunkte von Kreisen, die die vorgegebenen Kreise berühren.
Zu drei Kreisen gibt es drei Kegelschnittpaare für die Mittelpunkte der Kreise, die jeweils zwei der vorgegebenen Kreise berühren.
Zwei Kegelschnitte schneiden  sich in bis zu 4 Punkten. Die Kegelschnitte von zwei der Kegelschnitt-Paaren schneiden sich in bis zu 16 Punkten.
Unter diesen Punkten gibt es bis zu 8 gemeinsame Schnittpunkte
sich in bis zu 4 Punkten. Die Kegelschnitte von zwei der Kegelschnitt-Paaren schneiden sich in bis zu 16 Punkten.
Unter diesen Punkten gibt es bis zu 8 gemeinsame Schnittpunkte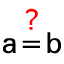 : dies sind die Mittelpunkte der gesuchten Berührkreise.
Unser Vorgehen für die "Konstruktion":
: dies sind die Mittelpunkte der gesuchten Berührkreise.
Unser Vorgehen für die "Konstruktion":
- Konstruktion der Mittellinien: je 2 konfokale Kegelschnitte
- Bestimmung der Schnittpunkte für je zwei Kegelschnitt-Paare
- Bestimmung der Berührkreise mit den gemeinsamen Schnittpunkten als Mittelpunkt.
Diese Akrivität ist eine Seite des GeoGebrabooks Zwei Kreise 20.05.2018, hinzugefügt: Sept. 2018
Zur Berechnung werden Listen verwendet, auch solche, die als Folge definiert sind (Folgen erleben wir oft als "zickig"!). Da Schnittpunkte oft komplex sind, d.h. reell nicht definiert sind, können sich Teile der Listen verflüchtigen, was Probleme bereiten könnte. Wie man schon bei den Mittellinien 2-er Kreise und bei der Animation der berührenden Kreise beobachten konnte, bereiten Geraden als Lösungen manchmal Probleme. Oft helfen kleine Verschiebungen der Ausgangskreise den Lösungen wieder auf die Sprünge. Die Konstruktionen verlangen bei der Auswahl der richtigen Teillösungen viel logische Kleinarbeit. Wir hoffen, dass nicht zu viele logische Fehlschlüsse verborgen sind. Ein Beispiel: ist der Mittelpunkt eines Kreises bekannt, der 2 vorgegebene Kreise berührt, so gibt es zu diesem Mittelpunkt 2 Kreise, die den einen vorgegebenen Kreis berühren. Welcher davon auch den anderen Kreis berührt, muss man prüfen: der Berührpunkt zweier Berührkreise zählt doppelt, der Schnitt zweier Kreise ohne Schnittpunkt ist nicht leer, sondern es ist {schneide(a,b)} -> { (?,?)}!