Problem 1_6
1_6
Construct the following diagram in which the circles and lines intersect tangentially.
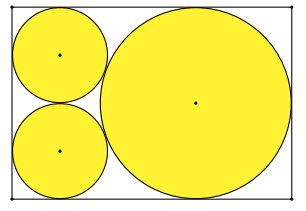
Solution:
I first started with the big circle. I then created a point (point B) on the right side of the circle and a line tangent to the circle. I then created two perpendicular lines to that one above and below (both intersecting the circle). Next, I created a parallel line to the line tangent to the circle to the left of the circle. I made points in which this parallel intersects with the line perpendicular to it (above (point C) and below (point D)). I also made the line segment connecting those two points. I then created the midpoint of this line segment (point E). I then created midpoints for line segments CE and DE. The midpoint of CE is point F and the midpoint of DE is point G. I then created a circle with center F and radius EF. I created an additional circle with center G and radius EG. I then closed the rectangle using a parallel line to the tangent line to the circle.