Angle Bisector Problem
I saw this post on Twitter and the nice non-trig solution offered up. It got me thinking about what other integer slopes besides 7 would have have angle bisectors with "nice" (rational) slopes.
How unique is 7? Do a lot of slopes work? Well, I did some investigating and found that between 2 and 10 million there are only nine integer values that work! 7, 41, 239, 1393, 8119, 47321, 275807, 1607521, 9369319.
How did I find these values? I let be the slope of the line which would mean the point would be on the line. I then let be a point on . In order to be isosceles, and thus . I then used excel to figure out which values of where integers (by subtracting the rounded values of then sorting by the difference... if the difference was 0, was an integer!).
It's easy to see that the angle bisector converges to a line making a angle with the x-axis. I noticed that the slope of the angle bisector seems to converge to 2.412... which seems like . Sure enough, the .
Since the slopes converge to , I then wondered if the partial evaluations of the continued fraction would be related to the slopes (I coach my school's math team and we were just playing around with continued fractions that same afternoon... the continued fraction for was still on the whiteboard!)...

The partial fractions are a sequence that alternate above and below on either side of and converge there as you go on and on...
It's interesting that the numerator of one partial is the denominator of the next... kind of like how ratios of Fibonacci Numbers converge on the Golden Ratio.

It ALSO turns out that these are the exact slopes of the angle bisector if the slope of the original line toggles between positive an negative! Wow! Very cool!
Can you work backwards to use these slopes to find the sequence slopes of the original lines? Hmm.
Here's the applet again. This time, the slope of the original line switches between positive and negative...
The answer the the question is "Yes! You can you work backwards to use these slopes to find the sequence slopes of the original lines!"
Using the tangent sum formula and the fact that the slope of a line is equal to the tangent of the angle it makes with the positive x-axis, you can derive that the slope of the original line, , can be written as a function of the slope of the angle bisector, :
Nice!
I used Excel to take it as far as it would let me... to evaluate the partial continued fractions then find the slope.... here's what it gave me:
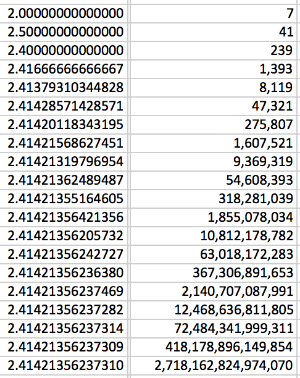
Are these numbers correct or did Excel lose it? Yes, some of them are and yes, Excel hit its limits.
It looks like each number is about 5.828427125 times the previous number until it isn't. Hmm. I think I need to check with a more accurate calculator.
I googled 5.828427125... turns out it's . Using this ratio in Excel and then rounding the results gave me this sequence of numbers:
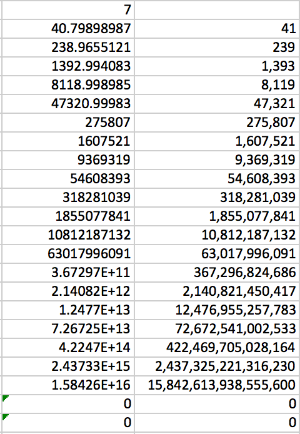
Yep, Excel did break... but it took longer than before.
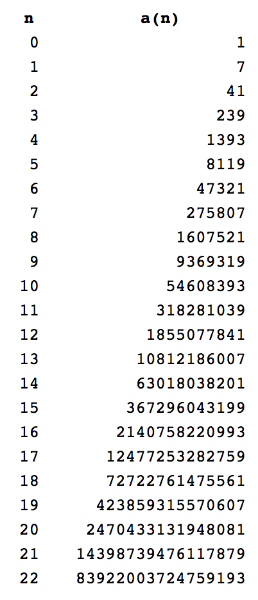
Some more googling and I discovered that this sequence is known as the NSW numbers (Newman-Shanks-Williams)
https://oeis.org/A002315
It turns out there's an explicit formula.
Using that this formula, I used Excel to create this list:
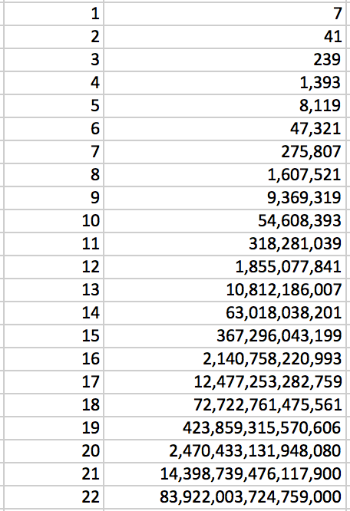
Correct? Possibly, however I trust the site about the NSW Sequence a bit more:
Cool... that was a fun worm hole to go down.
I just need a better calculator.