Il moto retrogrado secondo Tolomeo
Per spiegare i moti retrogradi dei pianeti, così come erano osservati da Terra, Tolomeo usò gli epicicli: suppose che ogni pianeta ruotasse con velocità costante su una traiettoria circolare (epiciclo), il cui centro a sua volta ruotasse con velocità costante su un’altra traiettoria circolare centrata sulla Terra (deferente). Regolando opportunamente i raggi dei due cerchi e le due velocità di rotazione si ottenevano le traiettorie salvando due principi considerati fondamentali: la Terra è al centro dell’universo; i moti dei corpi celesti sono costituiti da moti circolari.
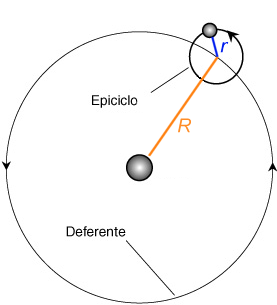
Costruzione:
1. Fissa il punto T = O (0,0). (T=TERRA)
2. Inserisci uno slider R che varia da 5 a 10, con incremento 1.
3. Disegna una circonferenza con il centro nel punto T e raggio R (DEFERENTE).
4. Prendi un punto sulla circonferenza, chiamalo B.
5. Inserisci uno slider r che varia da 2 a 5, con incremento 1.
6. Crea una nuova circonferenza con centro in B e raggio r (EPICICLO).
7. Prendi un punto P sulla nuova circonferenza. (P=PIANETA)
8. Costruisci una circonferenza con centro in T e raggio pari a 15 per rappresentare la sfera delle stelle fisse.
9. Ora traccia la semiretta con origine in T e passante per P. Sia S il punto di intersezione tra la sfera delle stelle fisse e la semiretta. Attiva la traccia per S.
10. Inserisci uno slider n che varia da 2 a 8, con incremento 1. Questo slider ci permetterà di variare la velocità di P.
11. Modifica la velocità del punto P. Con il tasto destro del mouse seleziona: Impostazioni – Algebra – Velocità, e inserisci il valore n.
12. Attiva la traccia del punto P.
13. Anima i punti P e B con il tasto destro del mouse.
Potrai facilmente vedere come Tolomeo spiegò il moto retrogrado dei pianeti.