Keeping It Real
Is he for real?

OBJECTIVE: To learn about the set of real numbers
So far, you've been studying sets in a general context. In this lesson, you'll learn about the set of real numbers and its subsets.
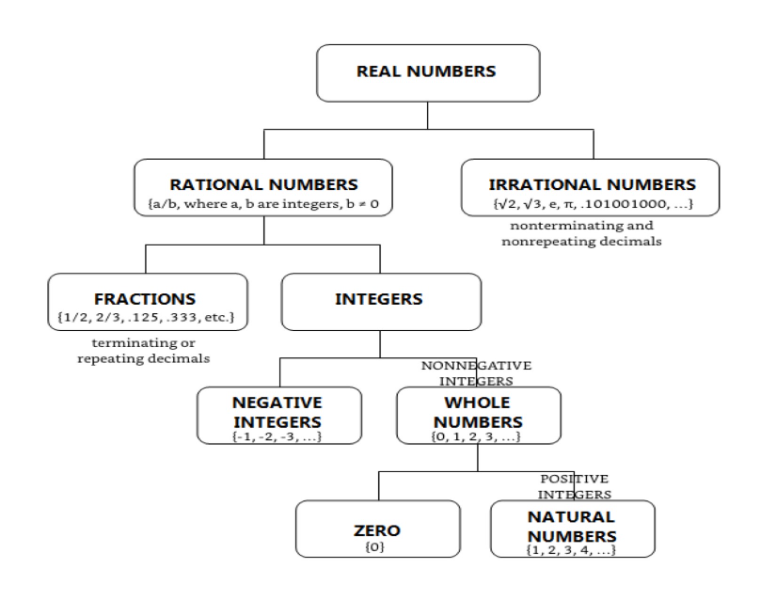
Below is a tree diagram of the set of real numbers. Let's study the real number tree from the roots.
At the root of the real number tree, we find the set of positive integers, also known as natural numbers or counting numbers. Beside it is another root containing a single element—zero. These two sets together form the set of whole numbers or nonnegative integers. If we add the set of negative integers to the set of whole numbers, we get the set of integers.
The set of integers is discrete, meaning each number in the set is individually separate and distinct. However, between any two integers is an infinite number of numbers, some of which may be fractions. Fractions may be written as a ratio of two integers (say  or
or  ) or as terminating or repeating decimals (0.5 for
) or as terminating or repeating decimals (0.5 for  or
or  for
for  ; the bar over 3 means the digit repeats indefinitely). Together, integers and fractions make up the set of rational numbers, whose main characteristic is that they can be written as a ratio of two integers. It's easy to see that
; the bar over 3 means the digit repeats indefinitely). Together, integers and fractions make up the set of rational numbers, whose main characteristic is that they can be written as a ratio of two integers. It's easy to see that  is a fraction, but how about 0 or 1? Well, 0 and 1 can be rewritten as
is a fraction, but how about 0 or 1? Well, 0 and 1 can be rewritten as  and
and  , respectively, so they also satisfy the definition of rational numbers.
Note, however, that not all numbers between two integers are rational; some are irrational numbers. The exact value of irrational numbers may be shown as radicals if they are real algebraic
, respectively, so they also satisfy the definition of rational numbers.
Note, however, that not all numbers between two integers are rational; some are irrational numbers. The exact value of irrational numbers may be shown as radicals if they are real algebraic  or as symbols if they are transcendental, such as π and e. Oftentimes, however, an estimate of these numbers up to the desired number of decimal places is used instead of the exact value since these numbers are nonterminating, nonrepeating decimals.
At the crown of the tree is the set of real numbers, which overarches the set of rational numbers and the set of irrational numbers.
or as symbols if they are transcendental, such as π and e. Oftentimes, however, an estimate of these numbers up to the desired number of decimal places is used instead of the exact value since these numbers are nonterminating, nonrepeating decimals.
At the crown of the tree is the set of real numbers, which overarches the set of rational numbers and the set of irrational numbers.
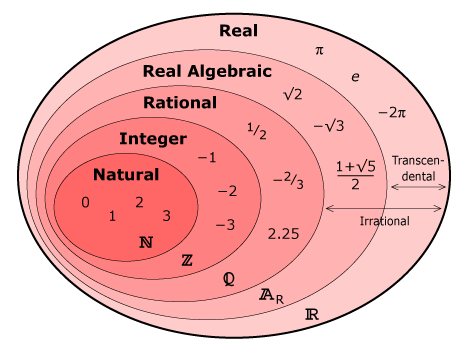
Another way of visualizing the set of real numbers is by means of a Venn diagram.
Below is a Venn diagram of the set of real numbers. Using set notation, N ⊂ (W) ⊂ Z ⊂ Q ⊂ AR ⊂ R.
NOTE: There is some disagreement among authors and texts in the treatment of the number zero. In the tree diagram above, zero is part of the set of whole numbers, but not of the set of natural numbers. In the Venn diagram below, zero is included in the set of natural numbers, which explains why there is no circle for the set of whole numbers. In this lesson series, we treat zero as a whole number, but not as a natural number. Hence, in the notation above, we have introduced the set of whole numbers, W, to include the set of natural numbers, N, and the unit set containing zero.
Below is a set of problems involving the set of real numbers and its subsets.
Set of Real Numbers and Its Subsets
Check the Answer Box below for the correct answers.
ANSWER BOX:
TODAY you learned about the set of real numbers and its subsets.
In succeeding lessons, you will explore the set of real numbers some more. Did you have FUN in today's lesson?
