Länge einer Kurve in 3D
Vorüberlegung
Die Entfernung eines Punktes vom Ausgangsort kann durch das Integral berechnet werden.
Ist ein Punkt am Ende der Bewegung wieder am Ausgangspunkt angekommen, so ist die Entfernung 0, der Punkt hat aber trotzdem einen bestimmte Weglänge zurückgelegt.
Die Länge des insgesamt zurückgelegten Weges wird deshalb durch bestimmt.
Zur Erklärung des Unterschieds von Entfernung und Weglänge siehe auch das Applet Entfernung und Weglänge.
Diese Überlegung führt auf die Berechnung der Länge einer Kurve (Weges) γ, die in Parameterform gegeben ist.
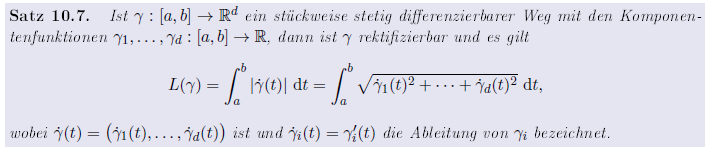
Eine anschauliche Begründung
Wie im Applet dargestellt ist, kann die Länge der Kurve näherungsweise durch einen Streckenzug bestimmt werden. Die Länge der einzelnen Strecken ergibt sich aus dem Satz des Pythagoras.
Beim Übergang für folgt daraus
Zur Berechnung der Länge eines Graphen von Funktionen f: ℝ → ℝ
Jede reelle Funktion kann geschrieben werden als .
Mit folgt daraus
.