área e função
(Obmep 2016, 1a Fase, Nível 3, Questão 11)
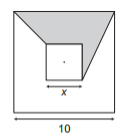
Os quadrados da figura (acima) têm lados paralelos e o mesmo centro. O quadrado maior tem lado 10 e o menor tem lado x. Qual é o gráfico que expressa a área da região cinza em função de x? (manipule o ponto que determina o valor de x no applet a seguir e use-o para responder a esta questão)
A curva mostrada pelo GeoGebra tem a aparência de uma parábola, então nesse caso teria-se que a área do polígono ABCDE é uma função quadrática, em x. Assim, caso de fato seja, poderia-se pegar três pontos – por exemplo (0, 25), (3, 28) e (5,25) – e encontrar a lei de formação desta função. Realize os cálculos e escreva a expressão que definiria a (suposta) função quadrática: (Obs.: use escreva x^2 para representar )
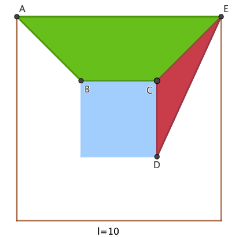
Uma solução para o problema acima poderia ser obtida, sem a ajuda do software, traçando o segmento EC para dividir a região cuja área (em cinza) é desejada em duas regiões disjuntas (um triângulo e um trapézio). Lembrando que a área do trapézio é e a área do triângulo é , encontre expressões para as áreas de cada figura separadamente e, depois, utilize-as para encontrar a expressão para a área do polígono ABCDE. Escreva as fórmulas de cada uma destas 3 áreas.