Simplex Algorithmus Dual Max 2 Min
Am Beispiel
3x+1,5y -> min
unter den Nebenbedingungen
I:20x+30y≥180000, II: 20x+30y≤210000, III: x+y=8000
Überführung in ein duales Programm das mit dem Max-Simplex-Algorithmus bearbeitet werden kann.
Die Nebenbedingungen von Min Systemen müssen auf die Form f(x)≥ b gebracht werden.
Ändere II in: -20x-30y≥-210000
und stelle die Daten in eine Matrix, die transponiert wird (tausche Zeilen/Spalten). Durch Einfügen von Basis/Schlupfvariablen zum einem Max Programm transformieren
(die Zielfunktion steht in der letzten Zeile - auch im Max-Simplex-Applet muß darauf geachtet werden: Zf->letzte Zeile):
 Das Applet SimplexAlgorithmusDualMax2Min.ggb erstellt aus einem Gleichungssystem (Nebenbedingungen, Zielfunktion in Gleichungen eingeben DualP) ein Duales Programm zur Minimierung DualTab, das mit Max-Simplex-Algorithmus gearbeitet werden kann.
Die Min-Gleichungen (b*10^3)
Ausgabe des Start-Tableau für ein duales Programm Min - Algorithmus Max-Programm
Start-DualTableau
PivotSpl=1, PivotZle=2
copy to A1
PivotSpl=3, PivotZle=2
copy to A1
PivotSpl=2, PivotZle=1
End-Tableau, Auswertung
Identifiziere an hand der 2./3. Spalte (gegen transponierten Lösungsvektor)
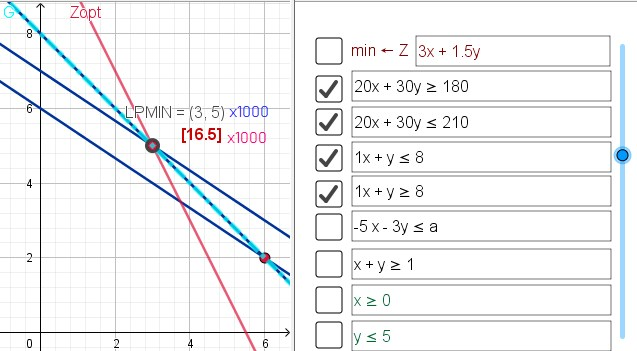
x=3000, y=5000, min->16500
Das Applet SimplexAlgorithmusDualMax2Min.ggb erstellt aus einem Gleichungssystem (Nebenbedingungen, Zielfunktion in Gleichungen eingeben DualP) ein Duales Programm zur Minimierung DualTab, das mit Max-Simplex-Algorithmus gearbeitet werden kann.
Die Min-Gleichungen (b*10^3)
Ausgabe des Start-Tableau für ein duales Programm Min - Algorithmus Max-Programm
Start-DualTableau
PivotSpl=1, PivotZle=2
copy to A1
PivotSpl=3, PivotZle=2
copy to A1
PivotSpl=2, PivotZle=1
End-Tableau, Auswertung
Identifiziere an hand der 2./3. Spalte (gegen transponierten Lösungsvektor)
x=3000, y=5000, min->16500
Grafische Lösung
JavaScript Demo Step by Step
Simplex Demo by Kenij Ikeda
Transscipt Example Data to: 30,-30,1,3/2; 20,-20,1,3; -180000,210000,-8000,0;
!enter fractions instead of decimal numbers, closing semicolon!
Ich hab nur das Eingabefeld für Daten ergänzt - sehr schön gemachte Schritt für Schritt Demo!
