Shine a light on Conic sections
Circle, ellipse, parabola, hyperbola and straight line (and point) are different shapes, somehow very different, but all belong to one family of conic sections (a.k.a. "conics"), i.e. the intersections between a cone and a plane. But why a cone? Why slicing a cone?
That's because of the projective nature of the light cone.

◯
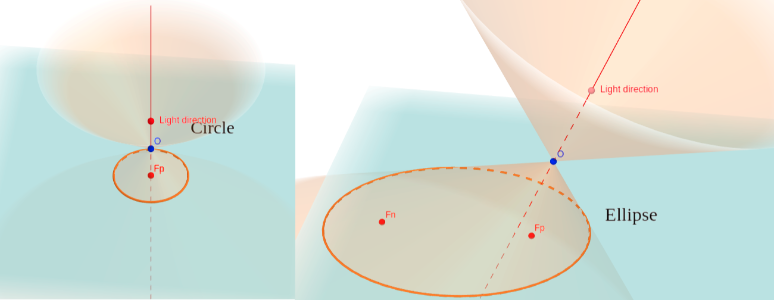
The cone and conics are all projections of circle the perfect shape:
- A cone is the shape of a circle projected prom one point (light source) into 3D space, like when you point a flashlight to the sky.
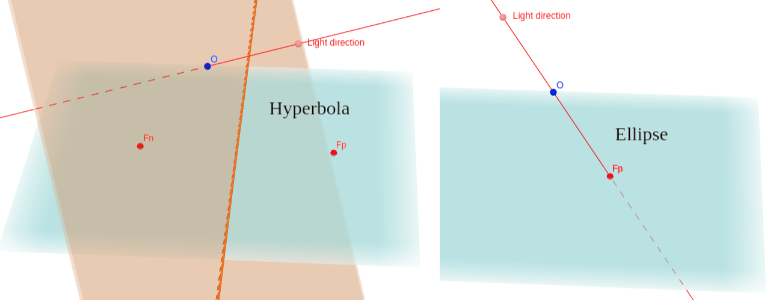
- A conic is the shape of a circle projected onto a plane (2D space), like when you shine a flashlight on a wall (to see ellipses) or on the street (to see hyperbolas). Because the boundary of the light cone of a normal (non-laser) flashlight is blur, it's better to place a coin in front of your light to see its shadow cast on wall or table top instead.
With aperture angle in range 0° < αo < 180° and projection angle αp ranging from 0° (perpendicular to the plane) to 90° (parallel to the plane), we have following projected images.
- Circle at αp = 0°: It's the original shape, only scaled (up).
- Ellipse when 0° < αp <
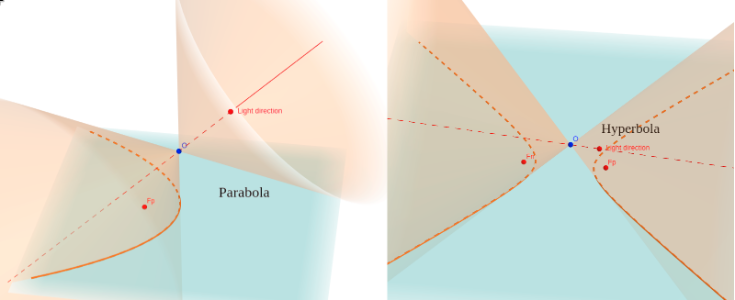
90° - : It's the slant view of circle that we usually . - Parabola at αp + =
90°: It's the transitional shape between ellipse and hyperbola, when the upper edge of light cone is parallel to the plane. It still comprises a single component like the ellipse, but it's already been open like the hyperbola. - Hyperbola when αp + >
90°: Its two branches are projection of the two opposite cones.
With aperture angle αo at two extremes, we have two degenerate shapes:
- Straight line at αo = 180°: It's a degenerate hyperbola, as the light cone degenerates into a plane.
- Point at αo = 0°: It's a degenerate ellipse, as the light cone degenerates into a straight line.
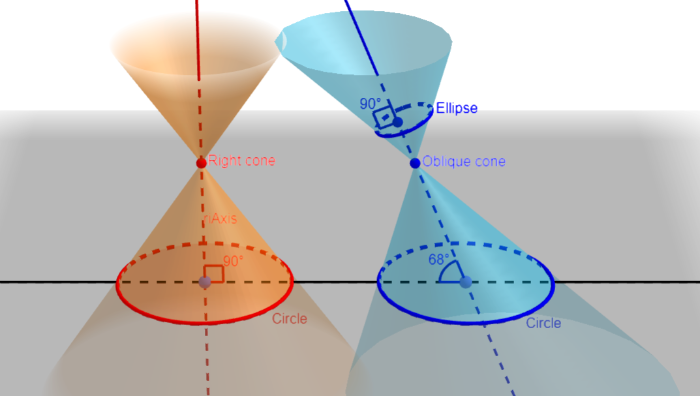
- αo = 0°: The generator circle degenerates into a point (south pole) on the sphere, and casts to a point of degenerate ellipse on the plane (shown as red points).
- 0° < αo < 180°: The generator circle is a small circle on the sphere, and casts to an ellipse, a parabola or a hyperbola on the plane. Smaller circles generate ellipses while larger circles generate hyperbolas, and the one in the middle generates parabola.
- αo = 180°: The generator circle is a great circle (equator) on the sphere, and casts to a straight line of degenerate hyperbola on the plane (shown as read circle and red line).

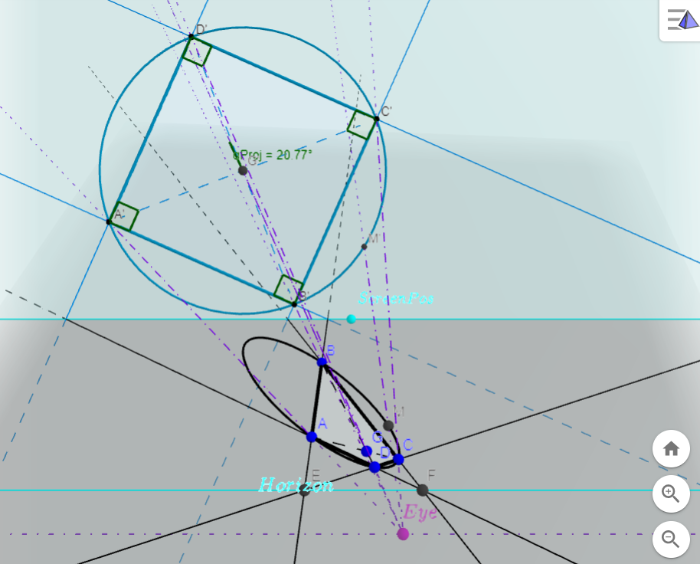
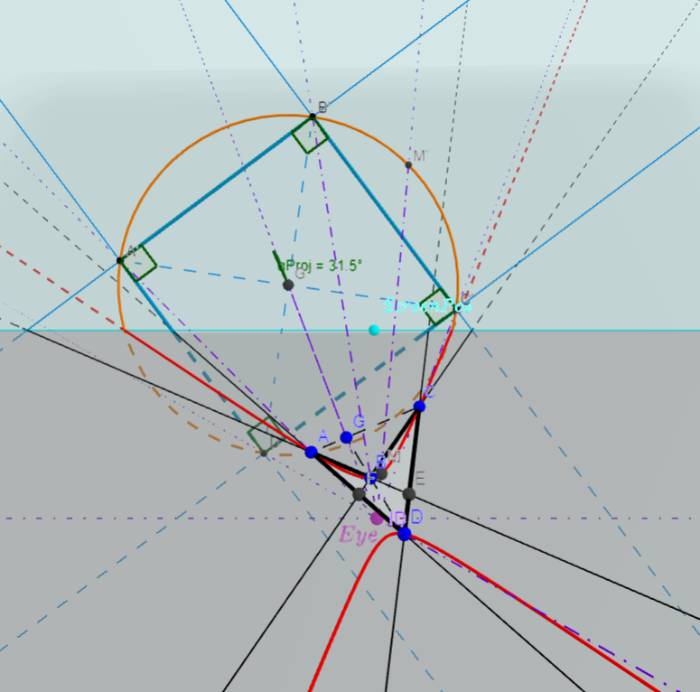
View cone and the unified image of conics
Have you ever wondered why the slant view of a circle is an ellipse?

Here we have to deal with the reverse direction:
- View cone is the projection of a conic in 3D space back into one point (the eye). This is similar to but not exactly the cone of vision (visual field) and the field of view.
- For any conic, there's a view cone projecting it into a circle.
Let's look at this 3D applet to see how an arbitrary conic is projected into a circle (and an arbitrary quadrilateral is projected into a square).