Alicia Boole Stott on cube, tetrahedra and octahedra.
From Appendix H of A new era of thought, page 216
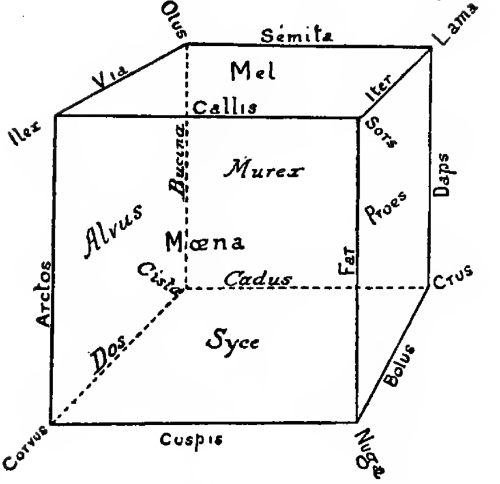
A tetrahedron may be regarded as a cube with every alternate corner cut off. Thus, if Mala have the corner towards Corvus cut off as far as the points Ilex, Nugae, Cista, and the corner towards Sors cut off as far as Ilex, Nugas, Lama, and the corner towards Crus cut off as far as Lama, Nugae, Cista, and the corner towards Olus cut off as far as Ilex, Lama, Cista, what is left of the cube is a tetrahedron, whose angles are at the points Ilex, Nugas, Cista, Lama. In a similar manner, if every alternate corner of a tessaract be cut off, the figure that is left is a tetra-tessaract, which is a figure bounded by sixteen regular tetrahedrons.
The octa-tessaract is got by cutting off every corner of the tessaract. If every corner of a cube is cut off, the figure left is an octa-hedron, whose angles are at the middle points of the sides. The angles of the octa-tessaract are at the middle points of its plane sides. A careful study of a tetra-hedron and an octa-hedron as they are cut out of a cube will be the best preparation for the study of these four-dimensional figures. It will be seen that there is much to learn of them, as — How many planes and lines there a
Model 1: Mala (in page 219 of A new era of thought)