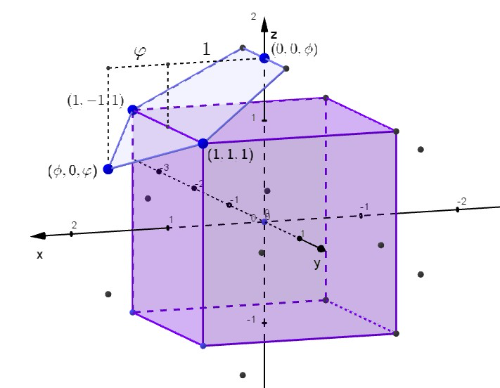
twaalfvlak rond kubus
een twaalfvlak rond een kubus
Een omgeschreven twaalfvlak rond een kubus is nog een mooi voorbeeld hoe je en terugvindt in een twaalfvlak.
- Construeer een kubus met als coördinaten van de 8 hoekpunten: .
- Bepaal daarrond 12 bijkomende punten met coördinaten: , waarin en .
- Deze 20 punten vormen de hoekpunten van een twaalfvlak. In het applet kan je het twaalfvlak opbouwen door de vijfhoeken rond de kubus aan elkaar te plakken.
Waarom komen die coördinaten zo mooi uit?
In de coördinaten van de hoekpunten van het twaaflvlak komen enkel 0, 1, en voor.
Het is een mooie toepassing van de eigenschappen van een vijfhoek.
Op de pagina PHI in een regelmatige vijfhoek werd reeds afgeleid dat de lengte van een diagonaal in een regelmatige vijfhoek met straal 1 gelijk is aan .
Analoog kan je ook een uitdrukking vinden voor de verhouding van de twee deellijnstukken waarin een diagonaal de zwaartelijn, loodrecht op de diagonaal, verdeelt. Beide eigenschappen vormen de sleutel voor de coördinaten van de hoekpunten van het twaalfvlak.
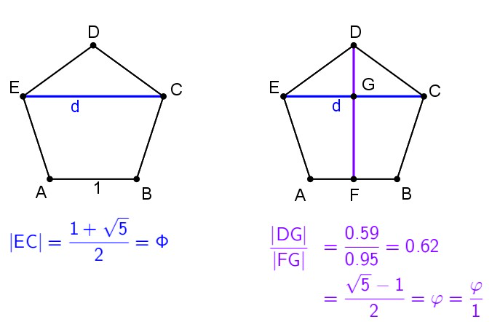
zijde en diagonaal
Bij de plaatsing van de vijfhoekige zijvlakken wordt telkens een diagonaal op een zijde van de kubus geplaatst.
De ribbe van de kubus is gelijk aan 2. Wat is dan de zijde van de overeenkomstige regelmatige vijfhoek?
In een regelmatige vijfhoek:
- komt een diagonaal met lengte overeen met een zijde 1.
- komt een diagonaal met lengte 2 overeen met een zijde
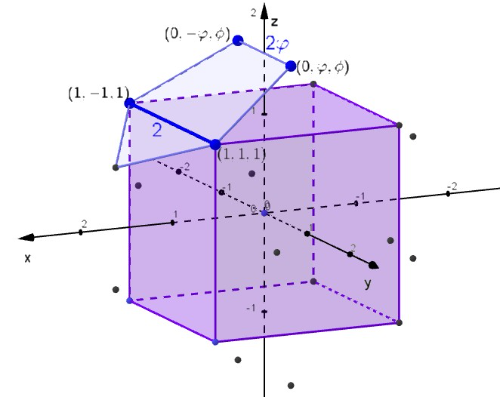
diagonaal en zwaartelijn
In onderstaande figuur zie je dat de lengte van het overstekende driehoekige stuk van de vijfhoek t.o.v. het deel boven het bovenvlak van de kubus inderdaad gelijk is aan .
Door te vertrekken van een kubus met ribbe 2 krijg je dus 's en 's in de coördinaten van de hoekpunten van het twaalfvlak.
Door de vijfhoek zo schuin te plaatsen dat het stuk boven het bovenvlak net de helft overdekt, zie je meteen dat je bovenaan, tegen de eerste vijfhoek aan, een tweede vijfhoek kan plaatsen.
En de z-coördinaten dan van deze hoekpunten?
Het topje van het uitstekende driehoekige stuk van de vijfhoek krijgt als x-coördinaat .
Wat je langs de horizontale x-as doet, doe je analoog t.o.v. de verticale z-as.
Plaats je tegen de kubus een vijfhoek met een uitstekend driehoekig stuk langs de z-as, dan zal dat topje een z-coördinaat krijgen, en samenvallen met een hoekpunt van de eerste vijfhoek.
Zo krijg je langs elk zijvlak van de kubus telkens 2 hoekpunten van het twaalfvlak, symmetrisch t.o.v. één van de assen.
Dezelfde redenering kan je toepassen op de andere ribben van de kubus, zodat de twaalf regelmatige vijfhoeken een twaalfvlak vormen.
Hoe schuin plaats je dus de vijfhoek op de kubus?
De hoek die de vijfhoek maakt met het bovenvlak van de kubus is eenvoudig te berekenen:
Met aanliggende rechthoekszijde 1 en overstaande rechthoekszijde vind je de hoek .