Parábola - Lección 04-01

Autor:profeDomingoHely Perez

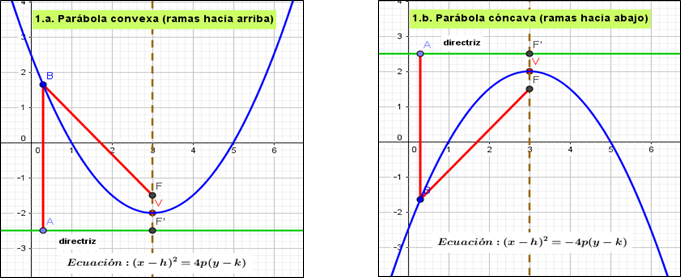
Parábola es el lugar geométrico de los puntos del plano tales que su distancia a un punto fijo llamado foco es igual a su distancia a una recta fija llamada directriz: distancia FB = distancia BA. Se muestran a continuación 4 imágenes de parábola: 1.a. Parábola convexa. Las ramas abren hacia arriba. Eje de simetría vertical. 1.b. Parábola cóncava. Las ramas abren hacia abajo. Eje de simetría vertical. 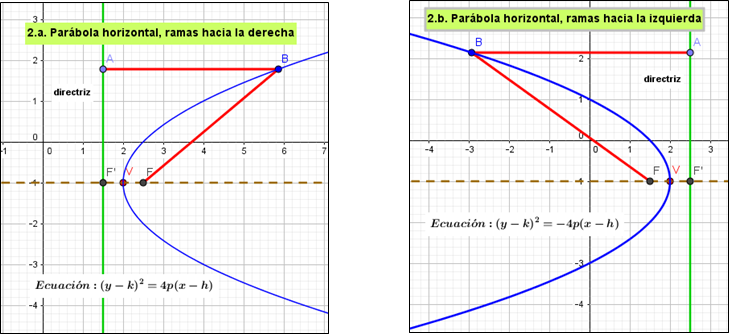2.a. Parábola horizontal, ramas abren hacia la derecha. Eje de simetría horizontal. 2.b. Parábola horizontal, ramas abren hacia la izquierda. Eje de simetría horizontal.

Elementos de la parábola. Vértice, V = (h, k): Es el punto extremo de la gráfica. También es el punto de intersección de la parábola y el eje focal o eje de simetría. Eje focal o eje de simetría: Es la recta que divide a la parábola en dos mitades congruentes. Pasa por el vértice y por el foco. Foco, F: Es el punto fijo de la parábola. Está ubicado sobre el eje focal a una distancia del vértice igual al parámetro p. Las coordenadas del foco dependen de las coordenadas del vértice, del parámetro y de la orientación de la parábola. Parámetro, p: Es la distancia entre el foco y el vértice o entre el vértice y la directriz. Su valor siempre es positivo porque es una distancia. Directriz: Es una recta perpendicular al eje focal a una distancia del vértice, igual al parámetro p. Radio vector, BF: Es cada uno de los segmentos que unen el foco con un punto cualquiera de la parábola. Por definición, el segmento BA tiene igual medida que el radio vector. Lado recto, MN: Es el segmento paralelo a la directriz y pasa por el foco. Los extremos M y N son puntos opuestos de la parábola. Su longitud es 4p. A continuación se presentan 4 applets, uno para cada orientación de la parábola.

Actividades: 1. Applet 1.a. Parábola convexa (ramas hacia arriba). Manipule los elementos interactivos del applet. El objetivo es generar la parábola. Para generar la parábola haga clic en el botón Activar rastro de B y a continuación, arrastre el punto A sobre la directriz. Para modificar la parábola, desactive rastro de B y borrar rastro. A continuación modifique los valores h, k y p. Características especiales de la parábola convexa (ramas hacia arriba) con vértice V = (h, k): a. Eje focal o eje de simetría: Es una recta vertical, paralela al eje Y. Cumple la fórmula x = h. Pasa por el vértice y por el foco. b. Coordenadas del Foco: Cumple la fórmula F = (h, k + p). El foco se ubica por encima del vértice. c. Ecuación de la directriz: Es una recta horizontal, paralela al eje X. Cumple la fórmula y = k - p. La directriz se ubica por debajo del vértice. d. Ecuación canónica de la parábola: Es una expresión de la forma

. El signo del coeficiente 4p siempre es positivo. Cuando el vértice de la parábola está en el origen, V = (0, 0), la ecuación canónica es

2. Applet 1.b. Parábola cóncava (ramas hacia abajo). Manipule los elementos interactivos del applet. El objetivo es generar la parábola. Para generar la parábola haga clic en el botón Activar rastro de B y a continuación, arrastre el punto A sobre la directriz. Para modificar la parábola, desactive rastro de B y borrar rastro. A continuación modifique los valores h, k y p. Características especiales de la parábola cóncava (ramas hacia aabajo) con vértice V = (h, k): a. Eje focal o eje de simetría: Es una recta vertical, paralela al eje Y. Cumple la fórmula x = h. Pasa por el vértice y por el foco. b. Coordenadas del Foco: Cumple la fórmula F = (h, k - p). El foco se ubica por debajo del vértice. c. Ecuación de la directriz: Es una recta horizontal, paralela al eje X. Cumple la fórmula y = k + p. La directriz se ubica por encima del vértice. d. Ecuación canónica de la parábola: Es una expresión de la forma

. El signo del coeficiente 4p siempre es negativo. Cuando el vértice de la parábola está en el origen, V = (0, 0), la ecuación canónica es

3. Applet 2.a. Parábola horizontal, ramas hacia la derecha. Manipule los elementos interactivos del applet. El objetivo es generar la parábola. Para generar la parábola haga clic en el botón Activar rastro de B y a continuación, arrastre el punto A sobre la directriz. Para modificar la parábola, desactive rastro de B y borrar rastro. A continuación modifique los valores h, k y p. Características especiales de la parábola horizontal, ramas hacia la derecha con vértice V = (h, k): a. Eje focal o eje de simetría: Es una recta horizontal, paralela al eje X. Cumple la fórmula y = k. Pasa por el vértice y por el foco. b. Coordenadas del Foco: Cumple la fórmula F = (h + p, k). El foco se ubica a la derecha del vértice. c. Ecuación de la directriz: Es una recta vertical, paralela al eje Y. Cumple la fórmula x = h - p. La directriz se ubica a la izquierda del vértice. d. Ecuación canónica de la parábola: Es una expresión de la forma

. El signo del coeficiente 4p siempre es positivo. Cuando el vértice de la parábola está en el origen, V = (0, 0), la ecuación canónica es

4. Applet 2.a. Parábola horizontal, ramas hacia la izquierda. Manipule los elementos interactivos del applet. El objetivo es generar la parábola. Para generar la parábola haga clic en el botón Activar rastro de B y a continuación, arrastre el punto A sobre la directriz. Para modificar la parábola, desactive rastro de B y borrar rastro. A continuación modifique los valores h, k y p. Características especiales de la parábola horizontal, ramas hacia la izquierda con vértice V = (h, k): a. Eje focal o eje de simetría: Es una recta horizontal, paralela al eje X. Cumple la fórmula y = k. Pasa por el vértice y por el foco. b. Coordenadas del Foco: Cumple la fórmula F = (h - p, k). El foco se ubica a la izquierda del vértice. c. Ecuación de la directriz: Es una recta vertical, paralela al eje Y. Cumple la fórmula x = h + p. La directriz se ubica a la derecha del vértice. d. Ecuación canónica de la parábola: Es una expresión de la forma

. El signo del coeficiente 4p siempre es negativo. Cuando el vértice de la parábola está en el origen, V = (0, 0), la ecuación canónica es

5. Applet para construir una parábola con eje focal vertical. Para construir la parábola se dan las coordenadas h, k del vértice y el valor del parámetro p. Utilice el deslizador PasoN para observar las instrucciones sucesivas necesarias para la construcción y haga uso de las herramientas disponibles. Para utilizar la barra de entrada, sólo es necesario escribir la instrucción o comando dado en los pasos 2 y 6. En el paso 2 para dibujar el foco, en la barra de entrada escribir F=(h,k+p) o F=(h,k-p). El punto que se dibuja recibe el nombre de F y toma las coordenadas h, k definidas con los deslizadores o casillas de entrada respectivas. En el paso 6 para activar el rastro del punto B, escribir Rastro(B,true) y para desactivar el rastro, escribir Rastro(B,false). El punto B es el punto de la parábola. Para generar la parábola, arrastre el punto A sobre la directriz. Para borrar el rastro mueva el plano cartesiano.

6. Applet para construir una parábola con eje focal horizontal. Para construir la parábola se dan las coordenadas h, k del vértice y el valor del parámetro p. Utilice el deslizador PasoN para observar las instrucciones sucesivas necesarias para la construcción y haga uso de las herramientas disponibles. Para utilizar la barra de entrada, sólo es necesario escribir la instrucción o comando dado en los pasos 2 y 6. En el paso 2 para dibujar el foco, en la barra de entrada escribir F=(h+p,k) o F=(h-p,k). El punto que se dibuja recibe el nombre de F y toma las coordenadas h, k definidas con los deslizadores o casillas de entrada respectivas. En el paso 6 para activar el rastro del punto B, escribir Rastro(B,true) y para desactivar el rastro, escribir Rastro(B,false). El punto B es el punto de la parábola. Para generar la parábola, arrastre el punto A sobre la directriz. Para borrar el rastro mueva el plano cartesiano.