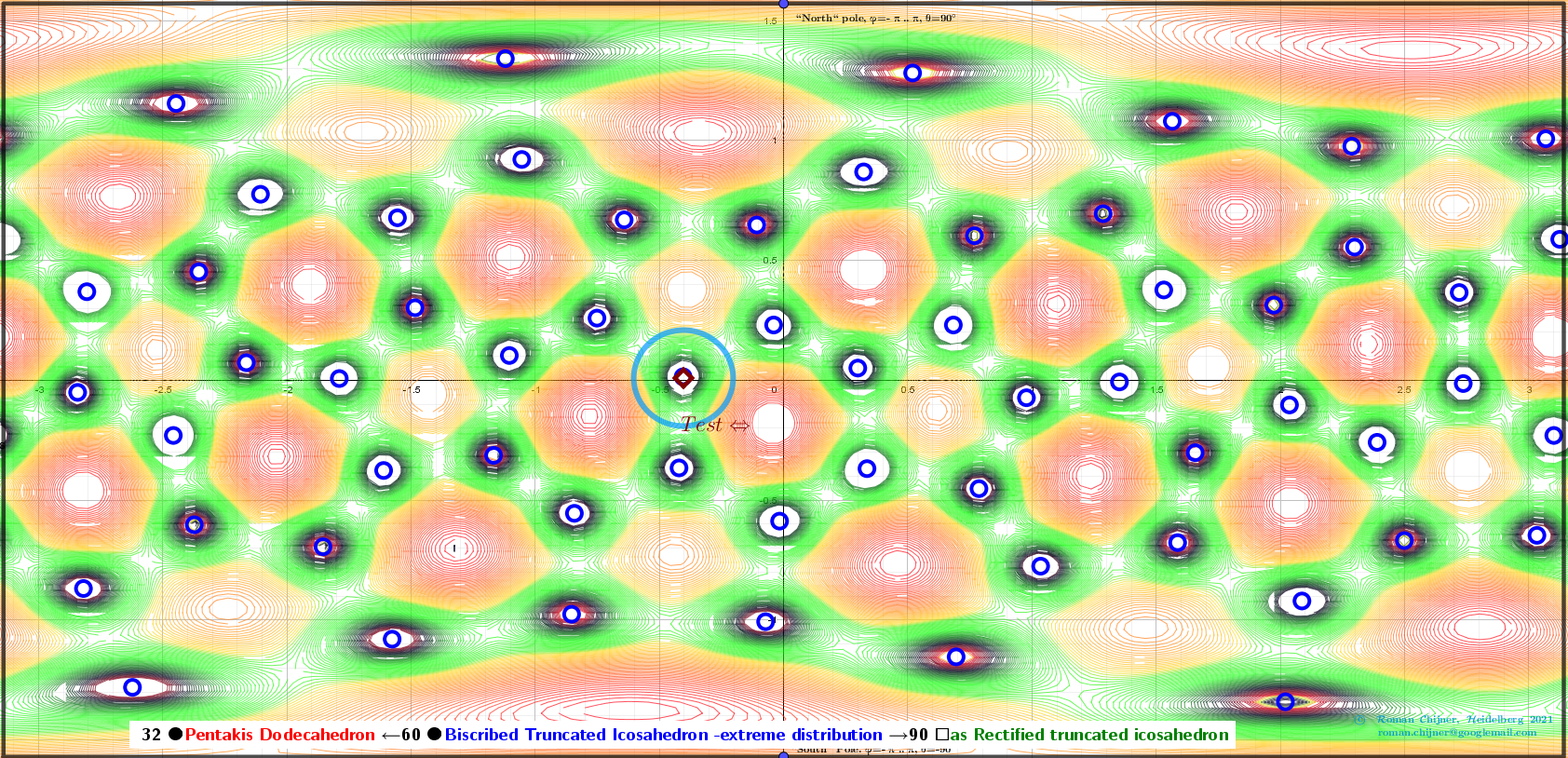
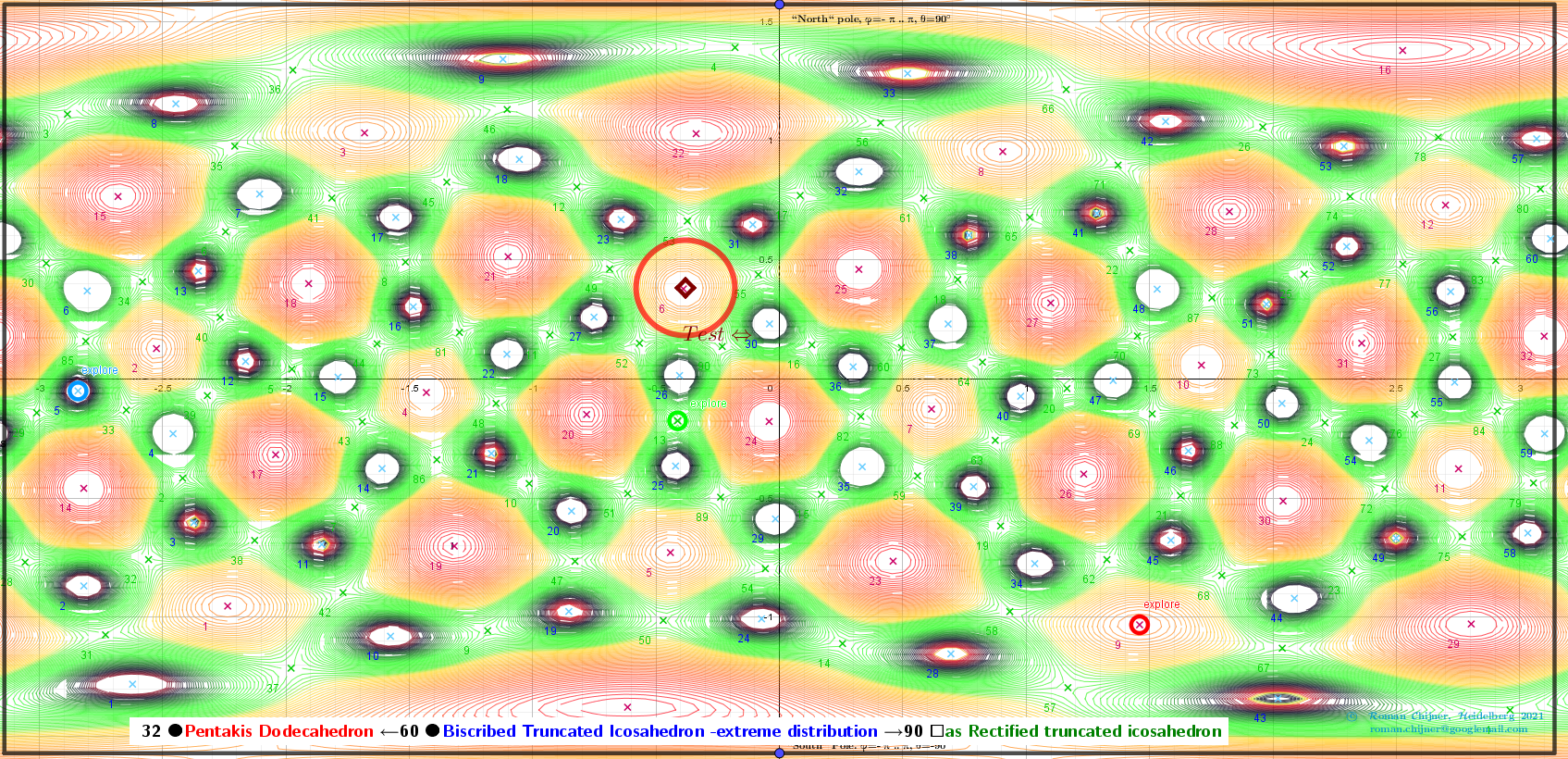
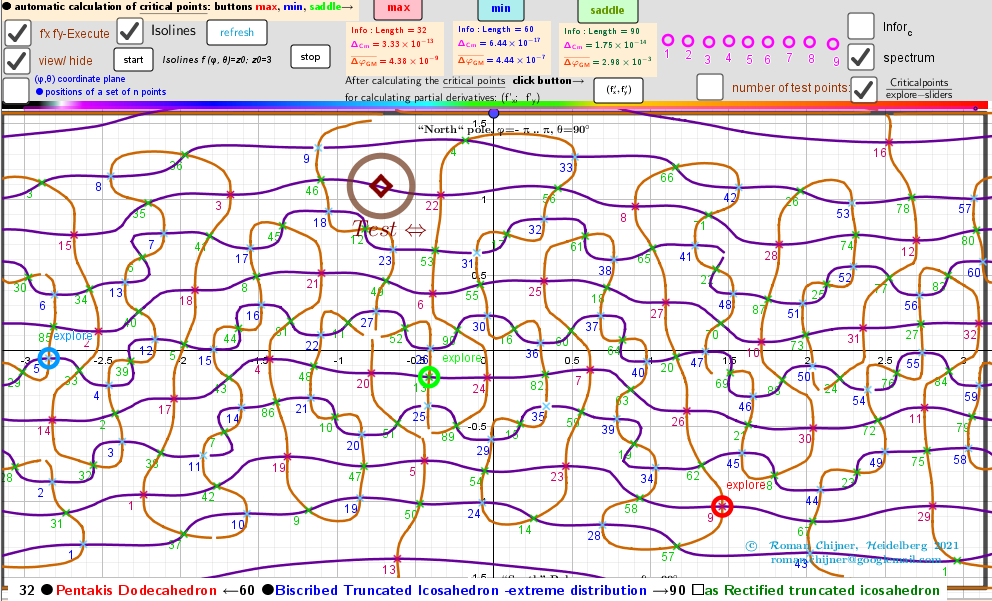
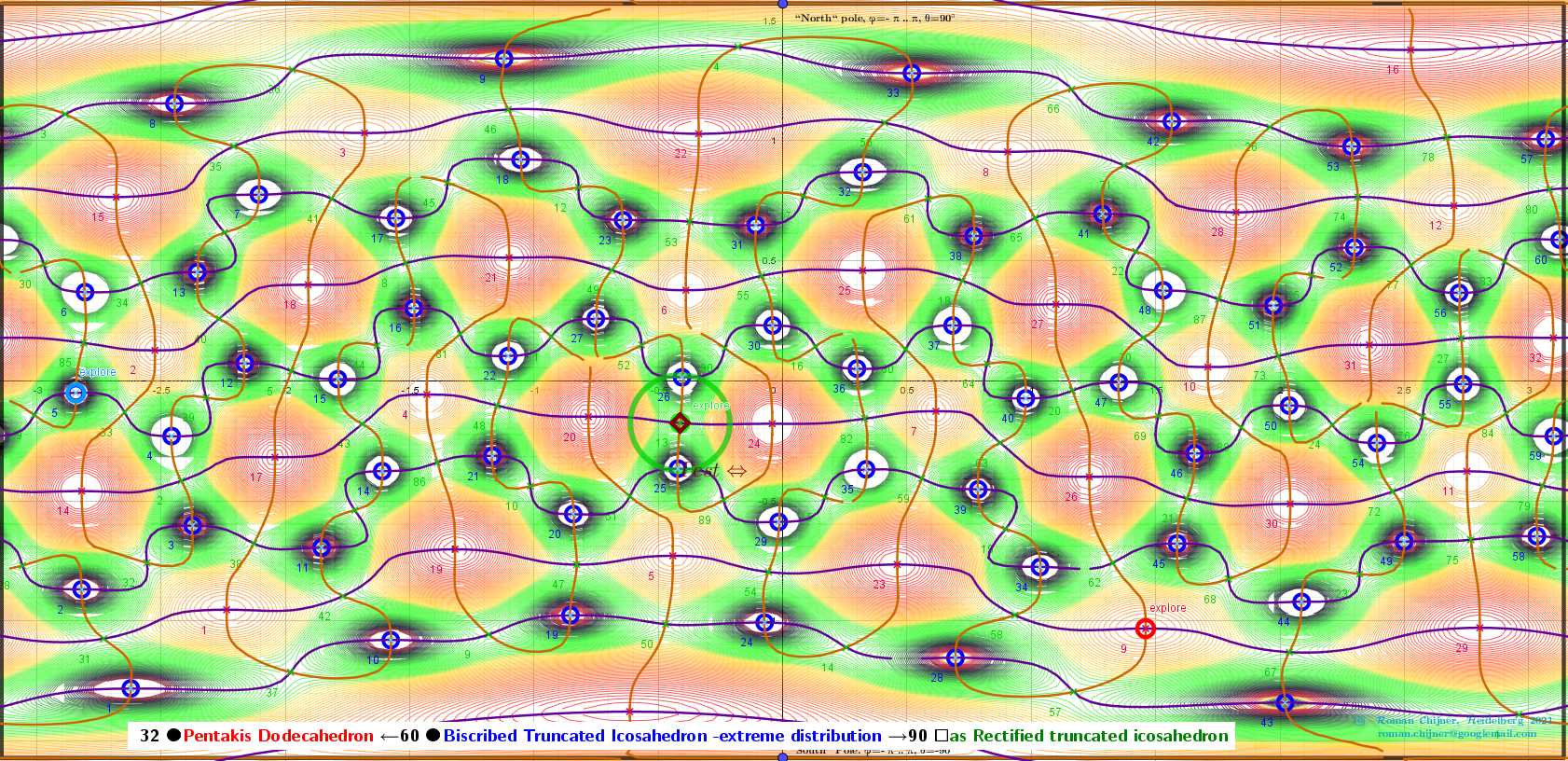
Vertices 60. Biscribed Truncated Icosahedron(extreme distribution). Images: A critical points scheme for Generating uniformly distributed points on a sphere.
The applet illustrates the case where 60 vertices of a Biscribed Truncated Icosahedron -extreme distribution "induce" the vertices of two other polyhedra:
32 ●Pentakis Dodecahedron ←60 ●Biscribed Truncated Icosahedron -extreme distribution →90 ☐ as Rectified truncated icosahedron.
Description are in https://www.geogebra.org/m/y8dnkeuu and https://www.geogebra.org/m/rkpxwceh.
Images and explanations of calculating results from applet: Generating two different uniformly distributed points on a sphere using one uniform distribution: Biscribed Truncated Icosahedron V=60:
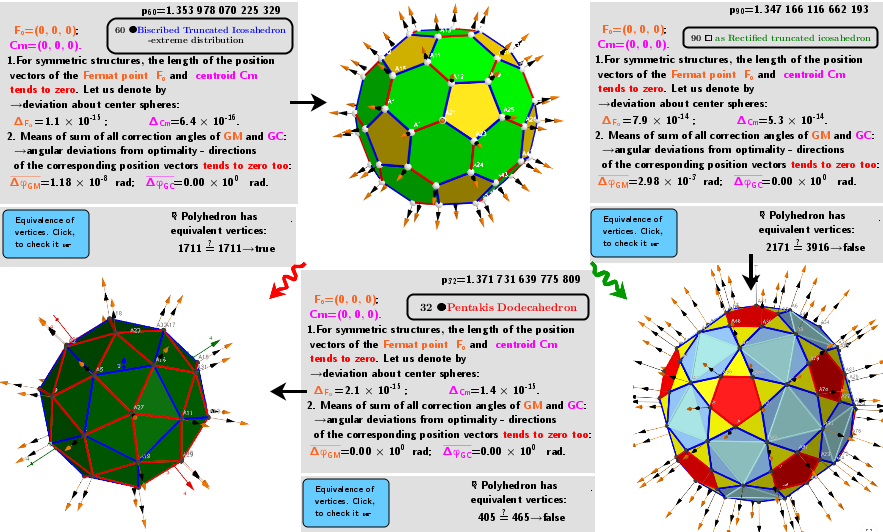
![“Polyhedra” of critical points:
[b]32 ●[color=#ff0000]Pentakis Dodecahedron[/color] ←60 ● [color=#0000ff]Biscribed Truncated Icosahedron -extreme distribution[/color] →90 ☐ [color=#38761d]as Rectified truncated icosahedron [/color][/b]](https://stage.geogebra.org/resource/nddcdyfd/GpkcHkDHXkXN8vJO/material-nddcdyfd.png)
Isolines, f'ₓ=0, f'ᵧ=0 and the critical points of the distance sum function over a rectangular region: - π ≤φ ≤ π; -π/2≤θ≤π/2.