Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

10-1 Classwork (Compositions)

Author:Russell Maciag
Image

More Practice

For each transformation, write it in both forms of notation.

Compositions of Transformations

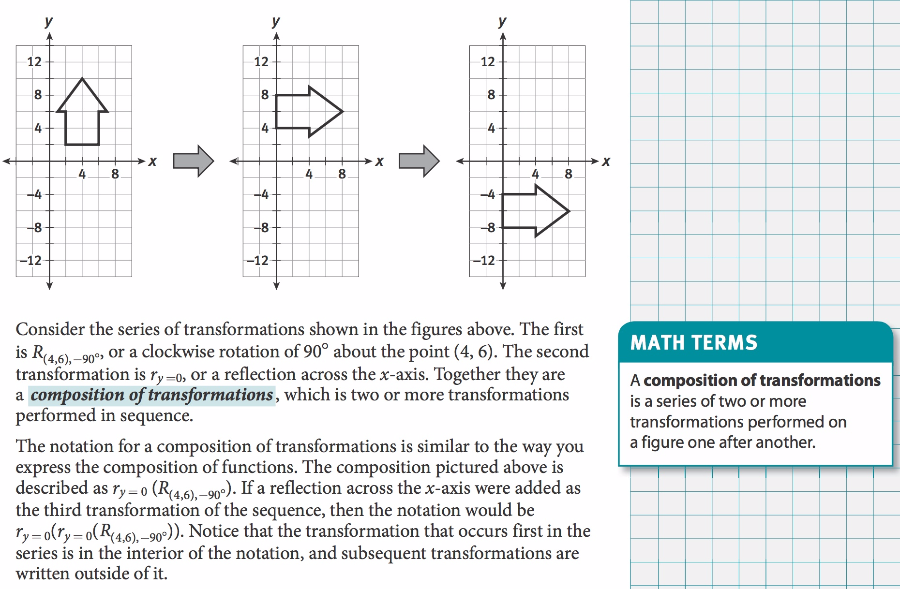
Learning Targets: * Find the image of a figure under a composition of rigid motions * Find the pre-image of a figure under a composition of rigid motions
Image

Moving on to a DIFFERENT EXAMPLE!!!

1. Write the notations for these compositions of transformations. Use the points A (0,0), B (1,1), and C (0,1).

A. A clockwise rotation of 60o about the origin, followed by a translation by directed line segment AB.

B. A reflection about the line x = 1, followed by a reflection about the line x = 2.

C. Three translations, each of directed line segment AC

The figure shows an arrow that points from a short horizontal line through (4,2) to its tip at (4,10). Using the graph below... 2. Draw the image of the arrow mapped by the composition r(x=4)(R(4,0),90). 3. Draw the image of the arrow mapped by the the same transformations in REVERSE order: R(4,0),90( r(x=4)).

4. What single transformation maps the arrow to image from #2? Write the name of the transformation and its symbolic representation.

5. What single transformation maps the arrow to image from #3?

As demonstrated by Items 2 and 3, the order of transformations in a composition can affect the position and orientation of the image. And as shown by Items 4 and 5, a composition can produce the same image as a single translation, reflection, or rotation. 6. For each of these compositions, predict the single transformation that produces the same image.

A. T(1,1)(T(0,1)(T(1,0)))

B. RO,90(RO,90)

C. r(x=0)(r(y=0))

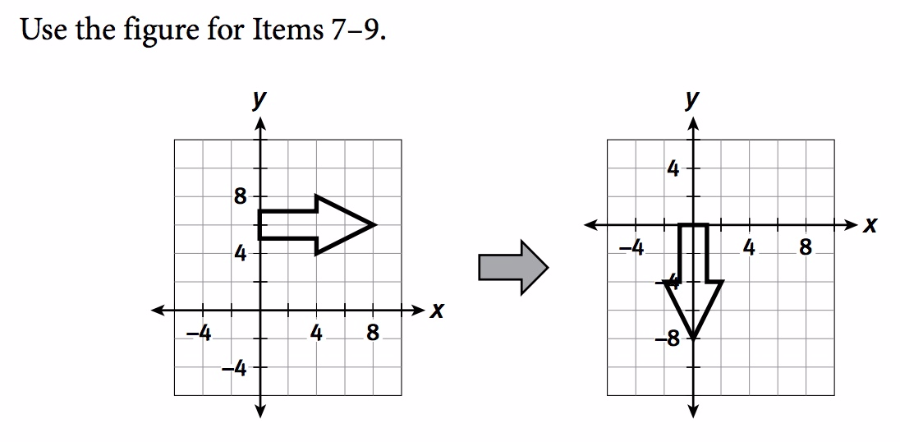
Image

7. Identify a composition of transformations that could map the arrow on the left to the image of the arrow on the right. Try in out by creating the area in the graph below then actually doing the transformations you listed.

8. Consider the composition you identified in Item 7 but with the transformations in reverse order. Does it still map the arrow to the same image? (Again try it out in the graph provided)

9. Identify a composition that undoes the mapping, meaning it maps the image of the arrow on the right to the pre-image on the left (this is referring back to the picture a few boxes up).

You can also find compositions of transformations away from the coordinate plane. 10. Points A, B, C, and D are points on the right-pointing arrow shown here. Predict the direction of the arrow after it is mapped by these compositions. Then test your prediction by completing this compositions on the graph below!

A. TDB(TAC)

B. rD'B'(RD,90)  ** Remember that the prime means the point AFTER the transformation! **

C. RA,180(rAC)

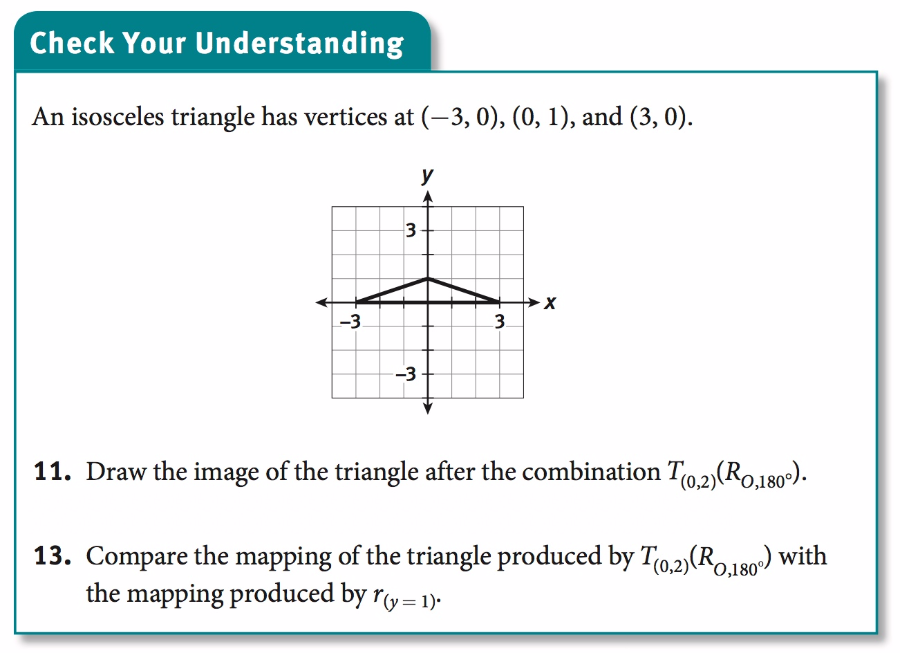
Image

Use this space to add any writing for numbers 11 and 13.

New Resources

Discover Resources

Discover Topics