Osobine grafika linearne funkcije
Neke osobine grafika linearne funkcije
Linearna funkcija je zadata u eksplicitnom obliku. Implicitni oblik ove funkcije glasi:
.
Koeficijent pravca date linearne funkcije je , a slobodan član linearne funkcije je .
Promenljiva naziva se nezavisno promenljiva, a promenljiva zavisno promenljiva.
Uočavamo da je presek grafika date linearne funkcije i -ose tačka (), a presek grafika linearne funkcije i -ose tačka ().
Vrednost nezavisno promenljive za koju je vrednost funkcije jednaka 0 naziva se nula funkcije.
Nulu funkcije računamo na sledeći način:
Ako je koeficijent pravca linearne funkcije pozitivan () funkcija je rastuća, a njen grafik zaklapa oštar ugao sa pozitivnim delom -ose.
Ako je koeficijent pravca linearne funkcije negativan () funkcija je opadajuća, a njen grafik zaklapa tup ugao sa pozitivnim delom -ose.
Uočavamo da grafik linerane funkcije zaklapa oštar ugao () sa pozitivnim delom -ose, pa je ova linearna funkcija rastuća.
Isto možemo zaključiti i bez crtanja grafika funkcije, na osnovu koeficijenta pravca:
Sa grafika takođe uočavamo i znak funkcije:
funkcija je pozitivna, tj. za (),
funkcija je negativna, tj. za ()
Kada je koeficijent pravca linearne funkcije jednak 0 (), linearna funkcija je oblika .
Linearna funkcija naziva se konstantna funkcija.
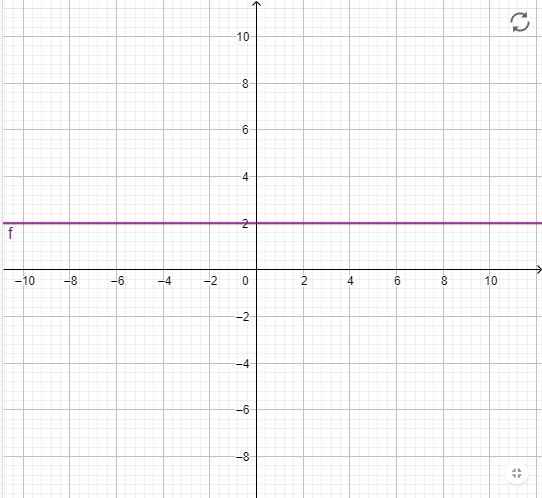
Konstantna funkcija , nema nulu i ne seče -osu.
Konstantna funkcija nije ni rastuća ni opadajuća, a njen grafik je paralelan -osi.
Konstantna funkcija y=n
Monotonost funkcije
Da li je linearna funkcija rastuća ili opadajuća?