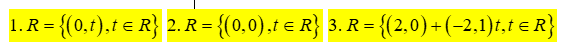Maticový zápis soustavy lineárních rovnic
V praktických aplikacích většinou volíme maticový zápis osustavy rovnic. Je přehlednější a je snadnější jej převést do syntaxe používaného software (Matlab, Maple,...). Rozepsání do složek vektoru neznámých provedeme roznásobením. Je třeba mít na paměti, že násobení matic není komutativní. Je rozdíl, zda je vektor neznámých x napsán zleva nebo zprava. Obvykle je volen zápis Ax = b a pokud není řečeno jinak, software toto pořadí činitelů předpokládá. Pokud je zadání ve tvaru součinu xA, rovnici transponujeme. Součin transponujeme transponováním každého členu a záměnou pořadí. A právě o to nám jde.
Příklad:
Určete všechna řešení homogenní soustavy lineárních rovnic
Řešení: Vynásobíme-li matici A vektorem neznámých x, dostaneme na levé straně rovnice vektor. Dva vektory se sobě rovnají, rovnají-li se všechny jejich složky. Pro vektory z R2 máme tedy dvě lineární rovnice pro dvě neznámé x1, x2.
Hodnost matice A je dva, protože řádky jsou lineárně závislé, odtud i rovnice jsou lineárně závislé a ve skutečnosti máme jej jednu lineární podmínku pro uspořídanou dvojici x1, x2. Řešení je nekonečně mnoho, závislých na jednom parametru. Zvolíme např. x1 jako reálný parametr t.
Řešení: Vynásobíme-li matici A vektorem neznámých x, dostaneme na levé straně rovnice vektor. Dva vektory se sobě rovnají, rovnají-li se všechny jejich složky. Pro vektory z R2 máme tedy dvě lineární rovnice pro dvě neznámé x1, x2.
Hodnost matice A je dva, protože řádky jsou lineárně závislé, odtud i rovnice jsou lineárně závislé a ve skutečnosti máme jej jednu lineární podmínku pro uspořídanou dvojici x1, x2. Řešení je nekonečně mnoho, závislých na jednom parametru. Zvolíme např. x1 jako reálný parametr t.
Příklady k procvičení
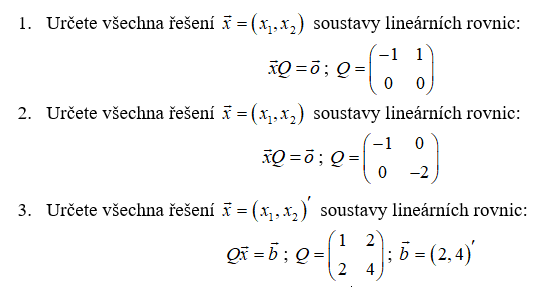
Příklad 1
Postup řešení
Všechny příklady jsou tak jednoduché, že ani není třeba používat nástroje GeoGebry 
Řešení je patrné ihned, z roznásobení x.Q. Pozor, nyní násobíme vektorem neznámých zleva, proto musí být zapsán v řádku, jinak by výsledný součin neexistoval.
Hodnost matice je jedna, tj. dostáváme jej jednu rovnici pro dvě neznámé a řešení tvoří jednoparametrický systém
.
Příklad 1(s GeoGebrou):
Stejný výsledek dostaneme i ze schodovité matice QTel (applet výše). Nejprve matici Q transponujeme, abychom vyměnili pořadí činitelů. Příkazem 
vidíme výsledek x1=0, tj. x2 může být jakékoliv reálné číslo.
SchodovityTvar pro určení Gaussovy eliminace.
Příklad 1 (bez software):
Řešení je patrné ihned, z roznásobení x.Q. Pozor, nyní násobíme vektorem neznámých zleva, proto musí být zapsán v řádku, jinak by výsledný součin neexistoval.
Hodnost matice je jedna, tj. dostáváme jej jednu rovnici pro dvě neznámé a řešení tvoří jednoparametrický systém
.
Příklad 1(s GeoGebrou):
Stejný výsledek dostaneme i ze schodovité matice QTel (applet výše). Nejprve matici Q transponujeme, abychom vyměnili pořadí činitelů. Příkazem SchodovityTvar(QT) získáme ekvivalentní matici QTel, z níž přepisem do soustavy rovnic
vidíme výsledek x1=0, tj. x2 může být jakékoliv reálné číslo.Řešení
