Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

5-3: Centroid & Orthocenter of a Triangle (with Euler Line)

Author:Rod Tolle

Handout for this activity.

Image

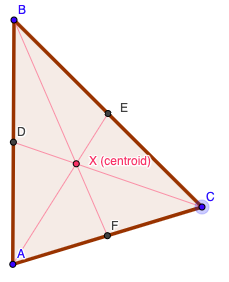
Locate the Centroid of a Triangle:

Locate the Orthocenter of a Triangle:

Part 2: Large Triangles (You may work on this with a classmate)
  1. Ask your teacher for a large whiteboard triangle
  2. Draw the three MEDIANS for the triangle (connect each vertex to the midpoint of the opposite side)
  3. Label the CENTROID of the triangle
  4. Try to balance the triangle at the centroid

Centroid Theorem: (using the LARGE TRIANGLE)


  1. Measure (in centimeters) and label the length of each segment of each median (6 segments total)
  2. Upload a picture of your triangle to Google Classroom
  3. Write a conjecture about the lengths of the segments you measured. Hint: compare BX to XF, AX to XE and DX to CX
		
>>> Record your conjecture on your handout paper.
Part 3: Euler Line

Use the applet below to answer the questions in this section.

Task 4
  1. Show only the Perpendicular Bisectors of sides (circumcenter)
  2. Drag a vertex to experiment with different types of triangles (scalene, isosceles, acute, right, obtuse, equiangular/equilateral)
Write a conjecture for the location of the CIRCUMCENTER of a triangle. Your conjecture could be like this:

The location of the circumcenter is _____ an acute triangle, _____ a right triangle, and _____ an obtuse triangle.  [choices: inside, outside, on]

>>> Record your conjecture on your handout paper.
Task 5
  1. Show only the Lines Containing Altitudes (orthocenter)
  2. Drag a vertex to experiment with different types of triangles (scalene, isosceles, acute, right, obtuse, equiangular/equilateral)
Write a conjecture for the location of the ORTHOCENTER of a triangle (inside, outside, or on the triangle). >>> Record your conjecture on your handout paper.
Task 6
  1. Show only the Angle Bisectors (incenter)
  2. Drag a vertex to experiment with different types of triangles (scalene, isosceles, acute, right, obtuse, equiangular/equilateral)
Write a conjecture for the location of the INCENTER of a triangle (inside, outside, or on the triangle). >>> Record your conjecture on your handout paper.
Task 7
  1. Show only the Medians (centroid)
  2. Drag a vertex to experiment with different types of triangles (scalene, isosceles, acute, right, obtuse, equiangular/equilateral)
Write a conjecture for the location of the CENTROID of a triangle (inside, outside, or on the triangle). >>> Record your conjecture on your handout paper.
Task 8
  1. Leave the centroid marked and show the centroid measurements.
  2. Test your hypothesis from Part 2: Large Triangles.
Did the measurements verify your hypothesis? If not, write a new hypothesis comparing the distances. >>> Record your conjecture on your handout paper.
Task 9 The Euler Line is named after an 18th century mathematician Leonhard Euler (pronounced 'oiler') Which of the four special points [orthocenter, circumcenter, incenter, centroid] are always on the Euler Line. (these points are collinear) >>> Record your conjecture on your handout paper.
Task 10 When is it possible for all four special points to be collinear? >>> Record your conjecture on your handout paper.
Task 11 When is it possible for all four special points to be concurrent? >>> Record your conjecture on your handout paper.

New Resources

Discover Resources

Discover Topics