Generación de polígonos estrellados con guion

Un polígono estrellado es un polígono que se construye a partir de un polígono regular al unir consecutivamente los vértices separados por un número fijo de vértices (salto) hasta llegar al primero. Reciben este nombre porque tienen forma de estrella. Para que sea efectivamente un polígono estrellado, todos los vértices del polígono regular original deben ser unidos, esto es, cuando vuelva al primer vértice por el que empecé a unir, debo haber unido antes todos los demás.

Observa, a continuación se presentan dos figuras, una de ellas tiene forma estrellada pero no es un polígono estrellado y la otra sí es un polígono estrellado.

Los polígonos estrellados se denotan por n/m siendo n el número de vértices del polígono regular convexo y m el salto entre vértices. El polígono estrellado de la Figura 2 se denotaría por 7/3.

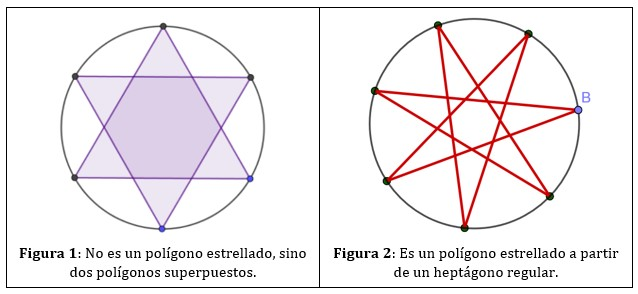
Mueve el deslizador n para elegir el polígono regular a partir del que vas a construir el polígono regular, y el deslizador Salto para elegir el salto (que sería el valor de m).

Abre en otra pestaña diferente de tu navegador el siguiente enlace: https://www.geogebra.org/m/z63cqune

¿Qué relación deben cumplir n y m para que el polígono estrellado n/m sea de verdad un polígono estrellado?

¿Por qué crees que la respuesta que has dado a la pregunta anterior es cierta?

¿En qué grado estás convencido (estas seguro de que es así) de que tu respuesta anterior es cierta? ¿Por qué?

Construye los polígonos estrellados 7/3 y 7/4. ¿Qué observas?

Dado un polígono regular con un número de lados n, ¿cuántos polígonos estrellados diferentes pueden formarse? Explica cómo llegas a esa conclusión.

A continuacion vamos a considerar el polígono que resulta de considerar toda la región del plano que queda dento del polígono estrellado, como en el ejemplo siguiente, al que vamos a llamar “polígono silueta”:

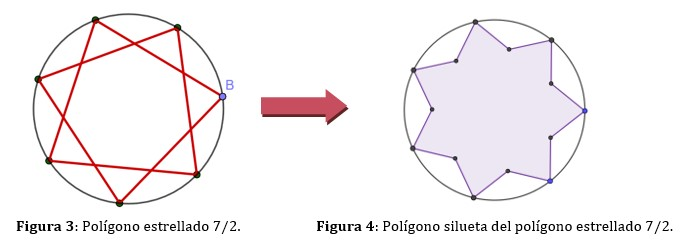
Observa el polígono silueta obtenido en la Figura 4. ¿Cómo son sus lados? ¿Y sus ángulos interiores? Calcula, sin medir, la amplitud de los ángulos interiores del polígono silueta de Figura 4.

Calcula los ángulos interiores del polígono silueta obtenido de los polígonos estrellados 12/5 y 13/6.

Generación de polígonos estrellados con guion

Mueve el deslizador n para elegir el polígono regular a partir del que vas a construir el polígono regular, y el deslizador Salto para elegir el salto (que sería el valor de m).

Nuevos recursos

Descubrir recursos

Descubre temas