Description. Finding Geometric Medians and Geometric Centers on a circle from discrete sample points.
Applet https://www.geogebra.org/m/qpmtdkuw is used to study the distribution of geometric medians and centers on the circle of radius R, „induces“ by the discrete sample of movable points in the x-y plane.
There is a set lP={p1, p2,...,pn} of points and {(xi,yi)∈ℝ²:i = 1,...,n} -their coordinates. Let a point (x,y) minimize a function of the sum of distances from this point to points lP. It is called Fermat's point https://en.wikipedia.org/wiki/Fermat_point or the Geometric median https://en.wikipedia.org/wiki/Geometric_median of the set lP.
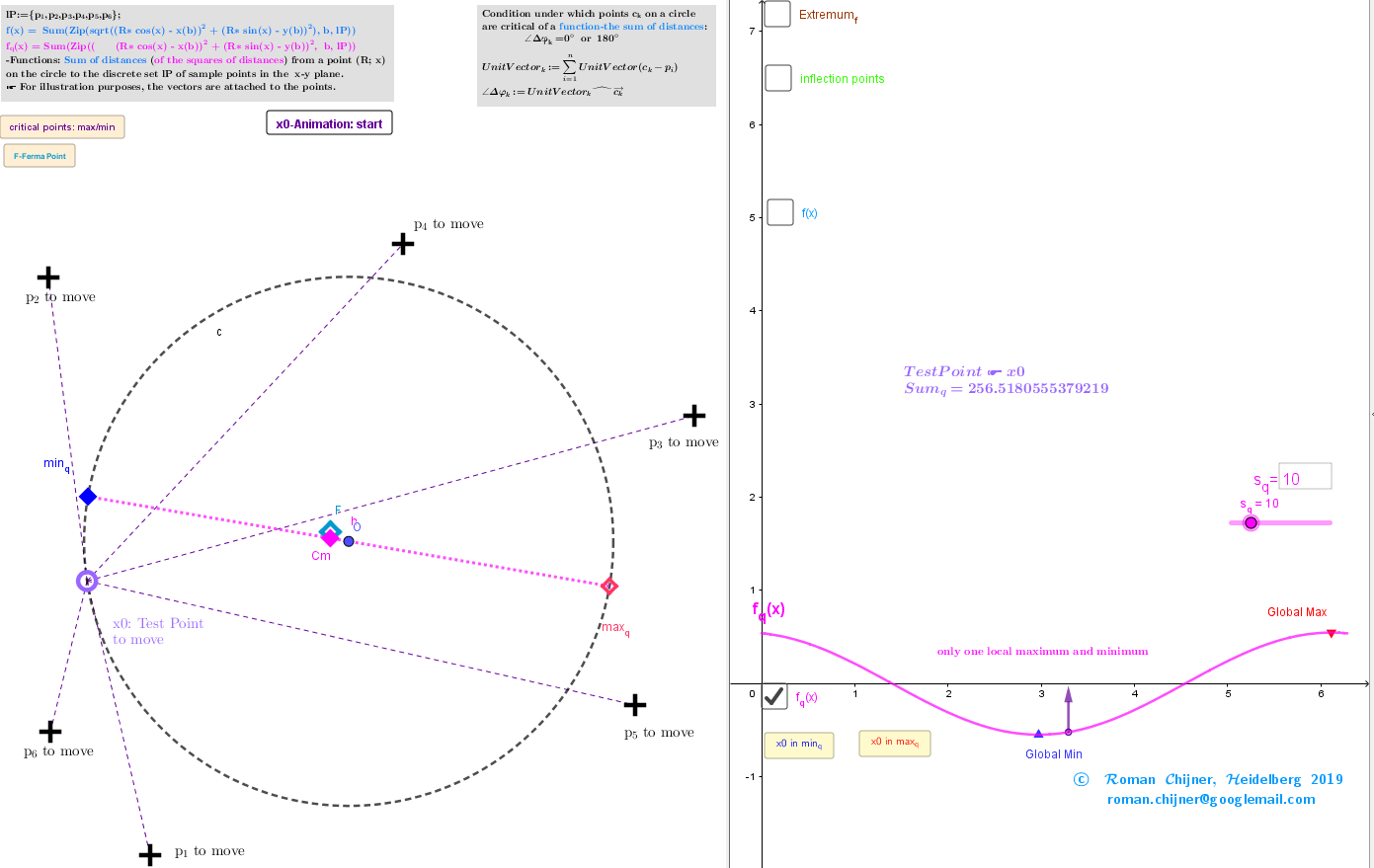
The point Cm minimizes a function of the sum of squared distances and is called the center of mass https://en.wikipedia.org/wiki/Center_of_mass, centroid or Geometric Center https://en.wikipedia.org/wiki/Centroid of the set lP.
Problem: find the positions of extreme points (and global minima and maxima too) of the function of sum (squares of the sum) of distances not on the entire x-y plane, but in its restricted region.
Definitions of geometric medians and centers can be generalized, in the sense that the extreme points of the sum (squares of the sum) of distances function searched in a restricted region of a x-y plane.
Geometric Medians in restricted region(circle)
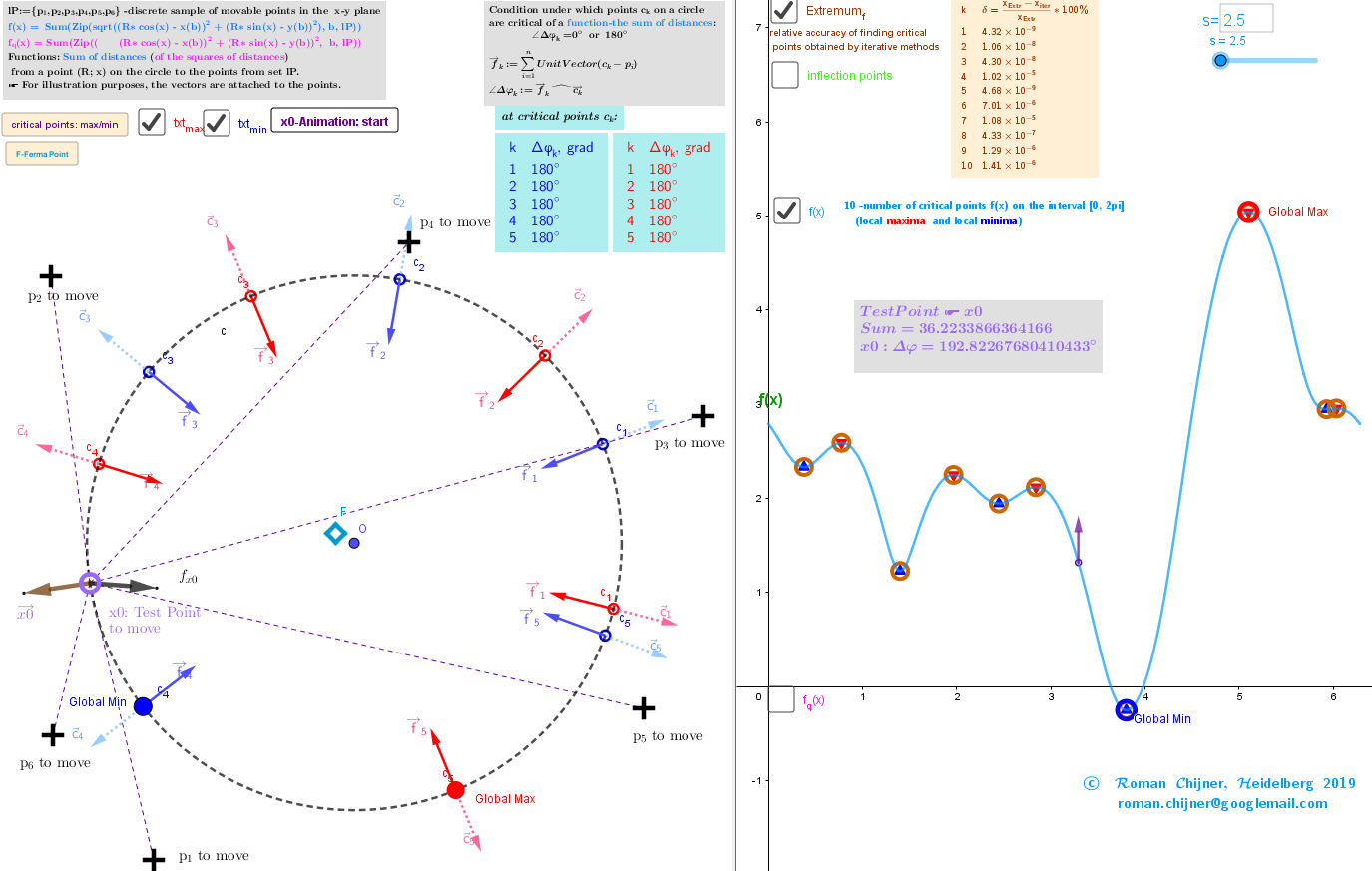
Iterative formulas
I propose iterative procedures in which each step produces is a more accurate approximation:
=R*UnitVector() finds the Maxima -c points and =R*UnitVector() finds the Minima -c points.
Geometric Centers in restricted region(circle)
Applets in a book:
Description. Finding Geometric Medians and Geometric Centers on a circle from discrete sample points.
Applet. Finding Geometric Medians and Geometric Centers on a circle from discrete sample points.
Method of Lagrange multipliers. Relative positioning of repulsive movable points on a circle.
Generating an extreme arrangements of points on a circle
Generating an extreme arrangements of points on a sphere
Generating an extreme arrangements of points on a sphere with more structured calculation program-GeoGebra Forum-
https://help.geogebra.org/topic/geogebra-windows-portable-zip-for-december