Normalabstand 2
Abstand des Punktes P von der Geraden g
1. Art:
- Lege durch P eine Normale h auf g.
- Bestimme den Schnittpunkt S der beiden Geraden.
- Berechne die Länge der Strecke [PS].
Aufgabe 1
Gegeben sind die Gerade g: A = (-2 | 4), und der Punkt P = (5,5 | 4).
a) Gib eine Parameterdarstellung von g sowie eine Normalvektorform von h an.
b) Berechne den Schnittpunkt S von g und h.
c) Berechne jetzt den Normalabstand d des Punktes P von der Geraden g.
2. Art:
- Bestimme einen Normalvektor von g.
- Projiziere den Vektor auf .
- Berechne die Länge der Projektion.
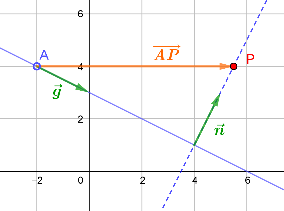
Aufgabe 2
a) Gib die Koordinaten von und an. b) Berechne die Länge d der Projektion von auf .