Esquema
Examples of Differentiability and Non-Differentiability
In this book, we see some visual examples for where functions are differentiable and non-differentiable.
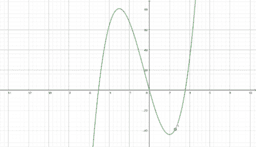
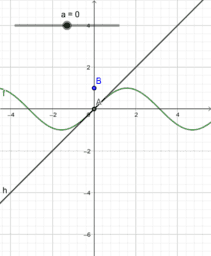
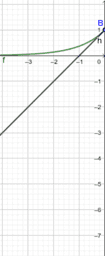
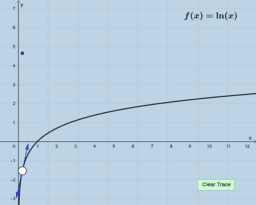
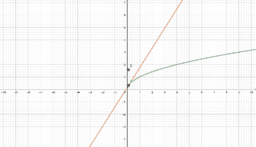
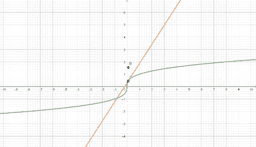
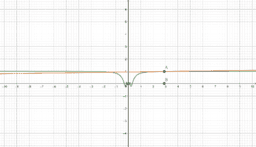
In essence, if a function is differentiable at a point, a non-vertical tangent line can be formed at said point. As such, if the function is differentiable, it must also be continuous at said point. In these instances, the function is smooth, and if we zoom in a lot, the function will begin to look linear and appear to overlap with the tangent line. We call this property local linearity, though we must beware the tricks our calculators and technology can play on us.
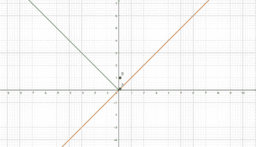
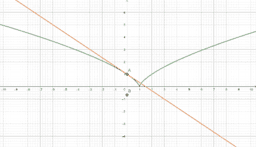
However, a function could be continuous, yet not differentiable at a point. In these instances, a function will have a sharp edge/corner, cusp, endpoint, or a weird oscillation preventing a limiting position for the tangent line near the point. If you look at a graph of the derivative in these instances, you will see some sort of discontinuity at said point (like a vertical asymptote or jump discontinuity). As such, if the derivative is not continuous at a point, the function cannot be differentiable at said point. This book provides easy to see visual examples of each.
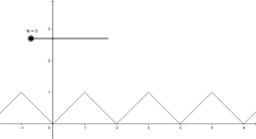
At the end of the book, I included an example of a function that is everywhere continuous, but nowhere differentiable. Can you tell why?