Series superpuestas: Cálculo de un punto doble conocido el otro
Figura de Análisis
Problema dual a este.
Este problema puede resolverse de dos maneras que emplean la misma figura de análisis (una tercera se describe más adelante).
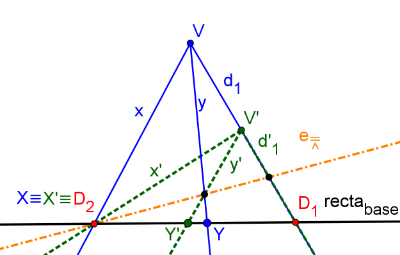
Si consideramos dos haces perspectivos, con base los puntos V y V', parejas de rayos homólogos se cortan en el eje perspectivo. Si se seccionan ambos haces con una recta base se obtienen dos series superpuestas. En estas series superpuestas aparecen dos puntos dobles, el primero en el corte del rayo doble d1=d'1 con la recta base. El segundo, en el corte del eje perspectivo de los haces con la recta base.
La metodología de resolución consiste en aplicar la figura de análisis al problema presente. Existen dos construcciones distintas. El punto doble, D1=D'1, es conocido. La primera construcción (deslizador "Construcción=1") es considerar dos haces perspectivos (de vértices V1 y V'1) cuyo rayo doble pase por dicho punto doble. Si determinamos el eje perspectivo de esos dos haces, su corte con la recta base determina el otro punto doble (mover el deslizador "Paso" para ver los distintos pasos de la construcción).
La segunda opción (deslizador "Construcción=2") es considerar un eje perspectivo que pase por el punto doble conocido. Si se proyecta una de las series desde un vértice V2 cualquiera, queda definido inmediatamente (con el eje perspectivo) el vértice V'2, y por lo tanto el rayo doble que corta a la recta base en el punto solución.
Por último, el problema se puede resolver empleando la propiedad de que los puntos dobles y los puntos límite de una proyectividad hiperbólica son isotómicos, es decir, tienen el mismo punto medio (deslizador "Construcción=3"). Si se separan las bases, con una recta paralela, la determinación del eje proyectivo permite determinar los puntos límites de manera inmediata, al ser el punto de corte entre s y s'' impropio. Determinando el punto medio de los límites se puede encontrar el otro punto doble.
Nótese que los puntos del enunciado se pueden mover.