Copy of Mod 7.1 Interior and Exterior Angles
Triangle Sum Theorem
Triangle Sum Theorem
Change the angles of the above triangle. What is the sum of all three interior angles of the triangle?
When will the sum of the interior angles of a triangle add up to 180 degrees?
Is it possible to create a triangle that the interior angles do not add up to 180 degrees?
Notice when the sides of the angles are adjacent and the vertices meet at one point, they form a straight angle.
What is the measure of a straight angle?
Take Note
How to find the sum of the interior angles of polygons. Be sure to pause video if needed and take notes.
Take Note:
Polygon Angle Sum
Using the slides on the above image, determine the sum of the interior angles of a dodecagon (12 sided polygon).
Using the slides on the above image, determine the sum of the interior angles of a hexagon (6 sided polygon).
Using the slides on the above image determine the sum of the interior angles of a pentagon (5 sided polygon)
![To determine the unknown angles of this pentagon we need to first determine the sum of the interior angles of a pentagon using the polygon angle sum theorem. (n-2)180[sup]o
[/sup]We determined that measure in the previous question and found the sum of the interior angles of a pentagon is 540[sup]o
[/sup]Write an equation adding up all interior angles and set it equal to 540[sup]o
[/sup]Solve for x[sup]o[/sup]](https://stage.geogebra.org/resource/xwajcvcr/sz2A7kbzllh8m2zT/material-xwajcvcr.png)
What is the measure of angle x in the pentagon above?
Take Notes as you watch video. Pause if needed.
Take notes, pausing video as needed. Also look for her mistake, one time she refers to opposite angles a and b as adjacent angles. Can you find the mistake?
Take note of Theorem

Solve the following
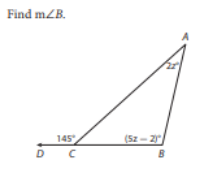
Looking at image above
What is the ? Set up the equation to solve for x. Solve for x, then substitute that value for x into the equation to determine the measure of angle B.
Solve the following.
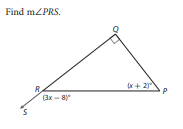
What is the ?
![Find the unknown angle measure x[sup]o[/sup]](https://stage.geogebra.org/resource/m8qxeuhf/Pn2wpmhiDSJonlAO/material-m8qxeuhf.png)
What is the unknown angle measure xo?
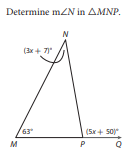
What is the from above?
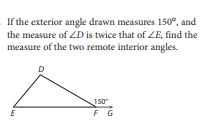
What is the measure of the two remote interior angles from above?