Legfeljebb hány részre osztja ...
- az egyenest n pontja;
- a síkot n egyenese;
- a teret n síkja;
- a k-dimenziós teret n darab k-1 dimenziós hitpersíkja ("Elvetemült geométereknek").
(Dr. Szilassi Lajos javaslatára)
1.
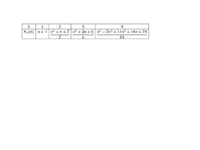
Tétel: az egyenest n pontja n + 1 részre (n -1 szakasz és két félegyenes) osztja. ezt így jelöljük:
. (Az R alsó indexe a dimenziószámra utal.) A tétel elég nyilvánvaló, aki akar, az gondolkodjon el a bizonyításon!
2.
Maximális számú síkrész akkor jön létre, ha az egyenesek között nincsenek párhuzamosak, különböző pontokban metszik egymást.
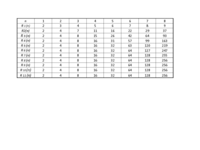
A fenti GeoGebra fájl alapján a keletkezett síkrészek száma:

Ismerősök ezek a számok?
Egészítsük ki a fenti táblázatot a háromszögszámok sorával!

A sejtés ...
ezek alapján már adódik: .
A bizonyítás ...
például teljes indukcióval (is) történhet.
n= 1-re igaz az állatás.
Tegyük fel, hogy adott a síkon n páronként nem párhuzamos egyenes, amelyek különböző pontokban metszik egymást, és  részre ontják a síkot. Egy (n + 1). egyenes egyikükkel sem párhuzamos és nem megy át a korábbiak egyik metszéspontján sem. Ezt az egyenest a korábbiak különböző pontokban metszik, és - a korábbiak szerint
részre ontják a síkot. Egy (n + 1). egyenes egyikükkel sem párhuzamos és nem megy át a korábbiak egyik metszéspontján sem. Ezt az egyenest a korábbiak különböző pontokban metszik, és - a korábbiak szerint  részre bontják. Minden így kapott egyenes rész két részre bont egy korábbi síkrészt. Ezek szerint:
Felhasználva az indukciós feltételt és a korábbiakat,
Az állítást bebizonyítottuk.
részre bontják. Minden így kapott egyenes rész két részre bont egy korábbi síkrészt. Ezek szerint:
Felhasználva az indukciós feltételt és a korábbiakat,
Az állítást bebizonyítottuk.
3.
Akkor osztja maximális számú részre a teret n sík, ha nincsenek közöttük párhuzamosak, különböző egyenesekben metszik egymást. és e metszésvonalak is különböző pontokban metszik egymást. Legyen adott n ilyen sík! Vegyünk hozzá egy (n + 1). síkot úgy hogy a korábbiakat a korábbiaktól különböző egyenesekben messe, és ne menjen át a korábbi metszésvonalak metszéspontjain! Ezt a síkot a korábbi síkok n egyenesben metszik, és a korábbiak szerint azt részre osztják. Minden ilyen síkrész két részre oszt egy korábban már meglevő síkrészt. Ezek szerint igaz a következő rekurzió:
.
Nyilvánvaló, hogy . Ennek és a korábbiaknak felhasználásával kapjuk, hogy

Egy jó sejtés kéne. Ennek megtalálásában segíthet a GeoGebra görbeillesztési funkciója:
Csak nem igaz az, hogy:
?
A bizonyítást az olvasóra bízzuk.
4.
"Elvetemült geométer" nem lévén, a korábbiak alapján csak egy rekurzió felvetését kockáztatjuk meg:
. (1)
Ha ezt a rekurziót helyesnek fogadjuk el, akkor a következőkre jutunk:

A sejtés megtalálásához megint illesszünk görbét!
Sejtés:
Ha igaz, akkor itt tartunk most.
Lehet, hogy érdemes böngészni.

Dr. Németh Zoltán tanár úr javaslatára ...
vizsgáljuk a következő sorozatot!
, ha .
A sorozat első néhány tagja:
Sejtés a fentiek alapján:
, ha
A bizonyítás - bizonyára - történhet az (1) rekurzió felhasználásával.
És még egy kérdés Dr. Németh Zoltán tanár úrtól:
Az rész között hány korlátos van?

Források:
- http://www.math.ubbcluj.ro/~andrasz/CD/INDUKCIO/III%20fejezet.pdf
- Pólya György: Indukció és analógia (Gondolat kiadó 1988. 60. oldal)