een toonstelsel door het stapelen van kwinten
Deze drie toontrappen I (do-C), IV (fa-F) en V (sol-G) vormen de basis van heel wat muziek.
Vraag het maar aan gitaristen. Met slechts drie akkoorden kan je heel wat populaire muziek begeleiden.
In de toonaard van C (do) zijn dit C, F en G.
In de toonaard van G (sol) zijn dit G, C en D
De drie toontrappen I - IV en V vormen ook de basis voor de klassieke harmonieleer.
"De vriend van mijn vriend is ook mijn vriend." Zo kan je het principe noemen waarmee ons toonstelsel is opgebouwd. Na het octaaf vormt de kwint de meest welluidende samenklank met de grondtoon.
Ook de kwint van de kwint zal welluidend klinken, enz. Door telkens de kwint te nemen van de laatst bekomen toontrap bouw je een toonstelsel op van 7 toontrappen.
Opmerking: door telkens een frequentieverhouding te nemen beland je al snel buiten het referentie-interval. Dat kan je oplossen door de bekomen verhouding te delen door 2.
Bijvoorbeeld:
- brengt je van grondnoot do naar kwint sol
- brengt je van kwint sol naar een toontrap in een volgend octaaf want . Maar en dat wordt de secunde re in het basisoctaaf. Deze methode blijf je nu herhalen.
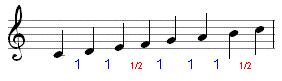
De opeenvolging van halve en hele tonen in onze toonladder is dus niet zomaar een willekeurige keuze.
Ze is het gevolg van een verdeling vanuit reine kwintverhoudingen.
Zouden we de twee halve toonafstanden samenvoegen de octaafafstand verdelen in 6 hele toonafstanden,
dan zou de toon met frequentieverhouding 3/2 niet eens in de toonladder zitten, terwijl ze juist de basis vormt.
Het denken in frequentieverhoudingen 2/1 en 3/2 is universeel en volgt uit het voorkomen van boventonen.
De verdeling van een octaaf in hele en halve toontrappen is geen keuze van Pythagoras.
Ze is een gevolg de aanpak om het basisinterval te verdelen: het gebruiken van de 3/2 verhouding.
Dit is een culturele keuze, net zoals het aantal stamtonen waarmee men werkt.
Wij zijn gewoon om melodielijnen te maken met 7 stamtonen. Het hadden er ook 5 of 8 of 9 kunnen zijn.
Stop je niet bij 7 tonen, dan kan je verder gaan tot het octaaf verdeeld is in enkel halve toonafstanden.
Maar dan begint het bouwsel van frequentieverhoudingen te wankelen.
Uit een pianoklavier zou je kunnen afleiden dat een interval van 12 kwinten gelijk is aan 7 octaven.
Want in kwintstappen belanden we na 12 kwinten op een si#.
Tussen si en do is maar een halve toon, dus de si# moet samenvallen met een do.
Maar dat blijkt toch niet zo mooi te kloppen als Pythagoras gehoopt had...
Want de frequentieverhouding van 12 kwinten wordt (2)7=128 en die van 7 octaven (3/2)12 = 129.7.
Binnen een octaaf is deze afwijking zo gering dat de 3/2- verhouding als perfect welluidend wordt ervaren.
Het probleem stelt zich bij wel bij het blijvend opeenstapelen van kwinten.
En ook binnen een octaaf heeft het zware gevolgen.
Zo wordt de terts berekend vanuit 4 opeengestapelde kwintverhoudingen.
Omdat hierbij ook de (geringe) afwijkingen opgeteld worden, zal de terts hoorbaar te hoog klinken.
De tertsverhouding 81/64 (= 1.2656) klinkt niet welluidend, want die breuk komt niet voor in de reeks
van natuurlijke boventonen. In deze reeks komt wel de verhouding 5/4 (= 1.25) voor t.o.v. de grondtoon.
Pythagoras negeerde daarom zijn terts en steunde enkel op kwinten en octaven.
Maar dat blijkt toch niet zo mooi te kloppen als Pythagoras gehoopt had...
Want de frequentieverhouding van 12 kwinten wordt (2)7=128 en die van 7 octaven (3/2)12 = 129.7.
Binnen een octaaf is deze afwijking zo gering dat de 3/2- verhouding als perfect welluidend wordt ervaren.
Het probleem stelt zich bij wel bij het blijvend opeenstapelen van kwinten.
En ook binnen een octaaf heeft het zware gevolgen.
Zo wordt de terts berekend vanuit 4 opeengestapelde kwintverhoudingen.
Omdat hierbij ook de (geringe) afwijkingen opgeteld worden, zal de terts hoorbaar te hoog klinken.
De tertsverhouding 81/64 (= 1.2656) klinkt niet welluidend, want die breuk komt niet voor in de reeks
van natuurlijke boventonen. In deze reeks komt wel de verhouding 5/4 (= 1.25) voor t.o.v. de grondtoon.
Pythagoras negeerde daarom zijn terts en steunde enkel op kwinten en octaven.