Elipse I
NOTA INICIAL
Ejercicio sugerido en Construcción 2.4 de MANUAL PARA GEOGEBRA Guías para geometría dinámica, animaciones y deslizadores [Alexánder Borbón A.]
Ejercicio propuesto
Al finalizar la Construcción 2.4 (Párabola como lugar geométrico) se proponía lo siguiente:
"Si se tienen dos puntos llamados focos y se sabe que la elipse está definida por los puntos que cumplen que la suma de la distancia del punto a los focos es constante, construya una elipse."
Conviene clarificar un poco más la cuestión, trayendo a colación los siguientes conceptos (extractados de Wikipedia):
Vamos a necesitar refrescar algunos elementos más...
"Como establece la definición inicial de la elipse como lugar geométrico, para todos los puntos P de la elipse la suma de las longitudes de sus dos radio vectores es una cantidad constante igual a la longitud 2a del eje mayor:"
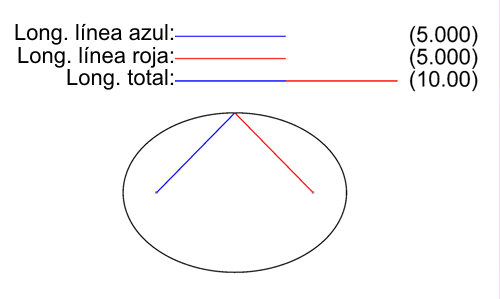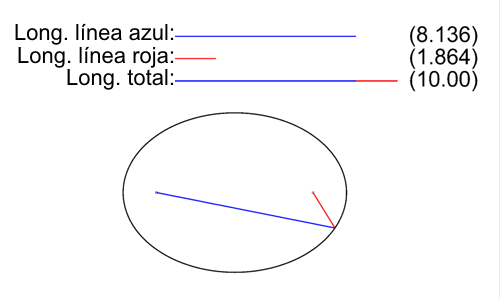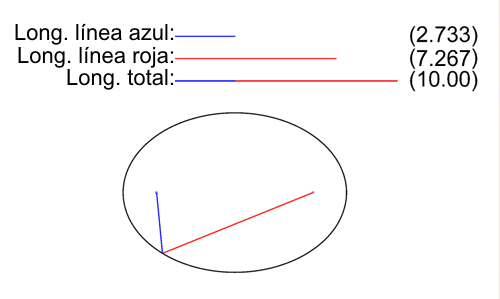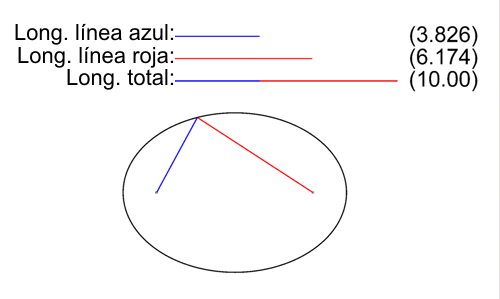 | NOTA: En la elipse de la imagen 2a vale 10 y se ilustra, para un conjunto selecto de puntos, cómo se cumple la definición. |
Elementos gráficos de la elipse
|  |
| La excentricidad ε (épsilon) de una elipse es la razón entre su semidistancia focal (longitud del segmento que parte del centro de la elipse y acaba en uno de sus focos), denominada por la letra c, y su semieje mayor. Su valor se encuentra entre cero y uno. |  |
Construcción paso a paso
Vamos a basar la construcción de nuestra elipse tomando como punto de partida el valor del semieje mayor a, y el de su excentricidad ε ; a partir de los mismos se pueden determinar los restantes valores.
- Active la herramienta Nuevo Punto
 y construya un punto O centro de la elipse; moviendo dicho punto se moverá toda la elipse en su conjunto.
Nota: Para cambiarle el nombre al punto se hace clic derecho sobre él y se escoje la opción Propiedades..., en la lengüeta Básico se le cambia el nombre.
y construya un punto O centro de la elipse; moviendo dicho punto se moverá toda la elipse en su conjunto.
Nota: Para cambiarle el nombre al punto se hace clic derecho sobre él y se escoje la opción Propiedades..., en la lengüeta Básico se le cambia el nombre. - Insertar dos deslizadores a y ξ con la herramienta
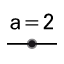 , que permitirán al usuario modificar las dimensiones del semieje mayor (de 0 a 10), y la excentricidad (entre 0 a 1).
, que permitirán al usuario modificar las dimensiones del semieje mayor (de 0 a 10), y la excentricidad (entre 0 a 1). - Vamos a determinar los dos puntos foco usando la barra de entrada; escribimos:
F1= (x(O) - ξ*a,y(O))yF2= (x(O) + ξ*a,y(O)) - Como vamos a emplear la idea de lugar geométrico para construir la elipse, necesitaremos una magnitud variable tal como se muestra en el gráfico superior; usaremos el radio vector asociado al foco F1 (línea azul), y llamaremos a su valor l1.
El deslizador tendrá un valor mínimo y uno máximo dependientes de las dos variables anteriores:
l1 mín:
a (1 - ξ)l1 max:a (1 + ξ) - Active la herramienta
 Circunferencia dado su Centro y uno de sus Puntos y construya una circunferencia c1 de radio l1 y centro F1 .
Circunferencia dado su Centro y uno de sus Puntos y construya una circunferencia c1 de radio l1 y centro F1 .
- Haga una segunda circunferencia c2 de radio ( 2a - l1 ) y centro F2. Este radio representa el valor l2 del otro radio vector (el asociado al foco F2).
- Vamos a determinar los dos puntos A y B de intersección entre ambas circunferencias usando la barra de entrada; escribimos:
Interseca(c1, c2)Recordemos que por la definición, ambos puntos pertenecerán a la elipse buscada - Escoja la herramienta
 Lugar Geométrico para construir el lugar que se forma por el punto A cuando el deslizador l1 (representando al primer radio vector) cambie de valor: tendremos así la parte superior de la elipse.
Lugar Geométrico para construir el lugar que se forma por el punto A cuando el deslizador l1 (representando al primer radio vector) cambie de valor: tendremos así la parte superior de la elipse.
- Repetiremos lo mismo pero tomando como base el punto B: conseguiremos ahora la parte inferior de la elipse.
- Opcionalmente podemos crear dos segmentos l1 y l2 que permitan visualizar la suma asociada a los radio vectores (cuando se mueve el punto A), y un texto que muestre que la suma de ambos segmentos es constante e igual a 2a.