2階線形同次は2次方程式のようなもの
2階線形微分方程式(2実数解)t=1,2
2階線形微分方程式(重複解)t=-1
2階線形微分方程式(複素数解)t=2±3i
1.定数係数2階線形
このワークシートはMath by Codeの一部です。
前回まで、微分方程式の基本となる1階線形の解法を扱ってきた。
今回は、同じ線形だけど、2階の場合について調べてみよう。
<定数係数の場合>
2階線形微分方程式の基本は定数係数だ。
2階のa、bが定数の線形微分方程式y"+ay'+by=0は2次方程式の解法に似ている。
等比数列の漸化式の単純化や行列の固有値を求めるのにも登場した
あの固有方程式、特性方程式が登場する。
固有方程式(特性方程式)t2+at+b=0の解がt=p,qのとき、
一般解は固有方程式の解の種別によって3タイプある。
・p,qが異なる実数ならy=Aepx+Beqx
・p=qの重複実数なら(p=-a/2)でy=(A x +B)epx
・複素数解p=m+ni, q=m-niなら、y=Aepx+Beqx=emx(C cosnx + D sinnx)
m=-a/2, n =√D/2
(理由)
y'+ky=0の解は、dy/dx=-kyを-1/ky dy=1 dxで変数分離すると、-1/k∫1/y dy=∫1 dxとなる。
-1/k log|y|=x+cから、 log|y|=-kx +d Cを定数とする一般解はy=Ce-kxと指数関数になる。
だから、y"+ay'+by=0 の1つの解をy=etxとおいてみる。
y'=t etx ,y'' = t2 etxとなる。
これをもとの方程式に代入すると、 t2 etx+a *t etx +b*etx =(t2 + at +b)etx となる。
だから、tが特性方程式(t2 + at +b)=0 の解なら、y=etxは微分方程式の解だといえるね。
・特性方程式が異なる実数解p,qを持つなら、2関数y1=epx, y2=eqxが微分方程式の解だから、
微積分の演算はベクトルのように線形だから、
この2関数を基底とした線形結合y=Ay1+By2が一般解となるね。
つまり、y=Aepx+Beqx
・特性方程式が重複実数解をもつなら判別式=0で、t=-a/2が重複解。
y1=e-ax/2、もう一つの解はy2=x*y1とするとy1に比例しない独立な基底にできる。
だから、y=Ay1+By2=Ae-ax/2 +Bxe-ax/2=(A+Bx)e-ax/2
・特性方程式が複素数解p=m+ni, q=m-niなら、
P=epx= emx+inx=emx einx=emx (cos nx + i sin nx)
Q=eqx= emx-inx=emx ei(-n)x=emx (cosnx - i sin nx)
(P+Q)/2=emx (cos nx)=y1 ,
(Q-P)/2i=emx (sin nx)=y2 とおくと、y2/y1=tan nx で、
一定ではないので独立基底とみることができる。
一般解はy=AP+BQ=Cy1+Dy2=emx (C cos nx+D sin nx)
(例)
「y" -3y’+2y=0の一般解」は?
固有方程式(t-1)(t-2)=0の解t=1,2から、y=Ae1x+Be2x
(例)
「y" +2y’+y=0の一般解」は?
固有方程式(t+1)2=0の解t=-1から、y=(Ax+B)e-1x
(例)
「y" -4y’+13y=0の一般解」は?
固有方程式の解t=2±3iから、y=e2x(A cos3x + B sin3x)
2.実装
質問:定数係数の2階線形微分方程式を解析的に解くコードはどうかけばよいでしょう。
<Sympy>
sympyで、y(n)(x)はDerivative(y(x), x, n)とかけます。
だから、
y''を変数ddyにDerivative(y(x),x,2)として入れて、
y'を変数dyにDerivative(y(x), x)として入れておくと、
微分方程式Eq(左辺, 0 )の左辺の中に使えます。
「y" -3y’+2y=0」y=Ae1x+Be2x
「y" +2y’+y=0」y=(Ax+B)e-1x
「y" -4y’+13y=0」y=e2x(A cos3x + B sin3x)
を確認しよう。
#[IN]Python
#===========================
from sympy.abc import *
from sympy import *
y = Function('y')
ddy=Derivative(y(x), x, 2)
dy=Derivative(y(x), x)
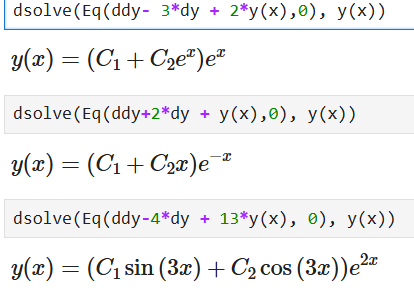
<geogebra>
geogebraでも常微分方程式が解けます。
それは、SolveODEです。
SolveODE(b(x), c(x), f(x), Start x, Start y, Start y', End x, Step)
Solves second order ODE y′′+b(x)y′+c(x)y=f(x).
とありますね。
「y" -3y’+2y=0」y=Ae1x+Be2x
「y" +2y’+y=0」y=(Ax+B)e-1x
「y" -4y’+13y=0」y=e2x(A cos3x + B sin3x)
を確認しよう。
SolveODEは、2階の場合は数値計算をして線をつないでいるようです。
1階ならば、設定がかなり少なくなるのは、解析的に解いて定数を代入するしくみなのでしょうね。
作った例が冒頭の3つのアプレットです。
SolveODE(b(x), c(x), f(x), Start x, Start y, Start y', End x, Step)
SolveODE(-3,2,0,-3,0.1,0.01,1,0.1)
SolveODE(2,1,0,-1,-4,8,4,0.1)
SolveODE(-4,13,0,-5,0,0.001,3,0.1)
と設定しておきました。
一般解の式のA,Bをうまくさがすと、ピッタリグラフが重なりますね。
同じgeogebraでもCASのSolveODEでは、解析に式を返します。
これでやってみましょう。
Sympyと同様に解析的に数式を返してくれます。
CASはすばらしい。
CASで定数係数2階線形微分方程式を解析的に解く
3.実例
<ばねの減衰しない振動>
ばねの長さの変化をしらべよう。
フックの法則F=-kx(ばねが自然長からxだけ引っ張るときに生まれる力Fはxに比例する)
ニュートンの運動方程式F=ma(等速度運動か静止を変更する力は物の質量と加速度の積に等しい)
この2つから、微分方程式を作りたい。つまり、空気抵抗などの邪魔がないときを考えてみよう。
変位xは時間tの関数で、加速度a=x''だから、mx''=-kx
つまり、x''+k/m x=0という2階線形微分方程式ができたね。
k/m=ω2とおくと。x''+ω2 x=0です。
初期値は、ばねの自然長さがx0、t=0の速度はv=0としましょう。
・特性方程式t2+ ω2=0の解は複素数解p,q=0±i ω
一般解はx=e0x(A cosωt + B sin ωt)
x= A cosωt + B sin ωt
・確認してみると、
v=x'=ω (A -sinωt + B cos ωt)
a=x''=-ω 2(A cosωt + B sin ωt)=-ω 2x
x''=-ω 2xが出ました。
これで、一般解がもとの微分方程式を満足させていることがわかりました。
・初期値はまだ使ってませんでした。
一般解x= A cosωt + B sin ωtで、
t=0と、x=x0から、x0=A cos0 + B sin 0=A速度v=ω (A -sinωt + B cos ωt)で、
t=0と、v=0と、A=x0から、0=ω (x0 -sin0 + B cos 0)=ω B 、ω≠0なので、B=0
ということは、x= A cosωt + B sin ωt= x0 cosωt
特殊解はx=x0 cosωt
このとき、v=x'=-ωx0 sinωt
ωt=2πを解くと、t=2π/ωですから、
この特殊解は、振幅x0で周期T=2π/ωの振動を表していますね。
振動数(周波数)は周期Tの逆数で、1秒間に1/T=ω/2π振動します。
単振動とか調和振動というものです。
・さらに、特殊解を分析してみよう。
v2=(-ωx0 sinωt)2=(ωx0)2(sinωt)2=(ωx0)2(1- (cosωt)2)= ω2(x02-(x0cosωt)2)=ω2(x02-x2)だから、
v2=(k/m)(x02-x2)
両辺にm/2をかけて、1/2mv2= 1/2kx02-1/2kx2
運動エネルギーがばねの弾性エネルギーの減少分に等しいことを言っています。
つまり、ばねについての力学的エネルギーが運動エネルギーと弾性エネルギーの和であり、保存されるということを言っているのですね。
<ばねの減衰振動>
空気抵抗を考慮するとどうなるだろうか。
空気抵抗は、ばねの先端のおもりの速さに比例して、変位と逆向きに働くから-cx'とおけるね。
mx''=-kx-cx'(m、k、cも正)Cは抵抗の係数になっている。
つまり、mx''+cx'+kx=0という2階線形微分方程式ができる。
初期値は、ばねの自然長さがx0、t=0の速度はv=0としましょう。
・特性方程式mt2+ct +k=0の解は場合分けが必要になる。解がt=p,qのとき、
一般解は固有方程式の解の種別によって3タイプある。
判別式はD=c2-4mk
①型・c2-4mkが正で、p,qが異なる実数ならx=Aept+Beqt
②型・c2-4mk=0で、p=qの重複実数なら(p=-c/2m)でy=(A t +B)ept
③型・c2-4mkが負で、複素数解p=a+bi, q=a-biなら、y=Aept+Beqt=eat(C cosbt + D sinbt)
a=-c/2m, b =√D/2
動きの特徴
①型・c2-4mkが正で、Cがどでかい。
m、c、kが正の2次関数f(t)=mt2+ct+kとf=0との交点がt=p,qになるとしよう。
f(0)=kは正。軸t=(p+q)/2= -c/2mは負。だから、p,qともに負となるね。
一般解は、x=Aept+Beqt
の指数部分pt, qtはtが正の時間でつねに負となる。ということは、tの増大により
exp(pt), exp(qt)は無限に0に近づく。
振動することなく、空気抵抗で押しつぶされる。
②型・c2-4mk=0で、Cがそこそこ大きい。
m、c、kが正の2次関数f(t)=mt2+ct+kとf=0との交点がt=p=qになるとしよう。
f(0)=kは正。軸t=(p+q)/2= -c/2mは負。だから、t=p=qは負となるね。
一般解はy=(A t +B)ept ①型と同様に振動することなく縮む。
③型・c2-4mkが負で、cは小さいので単振動に近いが、cは0ではないから減衰がある。
複素数解p=a+bi, q=a-biなら、y=Aept+Beqt=eat(C cosbt + D sinbt)
a=-c/2m, b =√-D/2
一般解y=exp(at)( C cosbt + D sin bt)で、t=0と、y=x0から、
x0=exp(0)(Ccos0 +Dcos0)=C。
速度v=y'=(eat)'(C cosbt + D sinbt)+(eat)(C cosbt + D sinbt)'
=a(eat)(C cosbt + D sinbt)+b(eat)(-C sinbt + D cosbt)
=exp(at){ (aC+bD)cosbt +(aD-bC)sinbt}
t=0と、v=0と、C=x0から、
0=exp(0){ (ax0+bD)cos0 +(aD-bx0)sin0} =(ax0+bD)なので、D=-x0 * a/b。
ということは、特殊解はx= eat(x0 cosbt -x0 *a/b sinbt)
(例)
初期値y0=0.15(m), 初速v0=0
質量m=89/9.8=9.082(kg),
復元定数k =890(kg/s2) ,
抵抗係数c=0から200としたときの
ばねの動きを予想しよう。
・c=0のときは単振動(調和振動)
k/m=890/(89/9.8)=98=ω2
ω=9.899
ω/2π=9.899/6.28=1.57555[Hz] 1秒の振動数
y=y0 cosωt=0.15 cos(9.899 x) が特殊解。
・c=200以下で減衰振動する範囲は?
f(t)=mt2+ct +k=9.082 t2+ct +890=0が複素数解をもつとき。
D=c2- 4*m*kが負, D' =-D
s=pow(4*k*m,1/2)
s=179.81078944268054
cが179.81078944268054以下のとき減衰振動になる。
c=100のとき、
a=-c/2m=-5.50539
b=√-D/2=pow(-c**2+4*k*m,1/2)/2m=8.22719
C=x0=0.15
D=-x0*a/b=0.10038
特殊解は
y= eat(x0 cosbt -a x0 sinbt)
=exp(-5.50539 x) (0.15 cos( 8.22719 x) + 0.10038 sin( 8.22719 x))