unit repeat
The construction of the geometric patterns is discussed and bears lots of speculation, more than historical evidence since there’s not one evident historical bible on Islamic architecture, no Vitruvius nor Alberti. However There’s the Topkapi scroll, the Tasjkent scrol land a document preserved in the Bibliothèque Nationale of Paris. Professor Jan Hogendijk published a dutch translation of a stepwise description of a unit repeat in the article Middeleeuwse Islamitische geometrische ornamentiek. In next applet we follow his translation and the construction of the pattern.

Now the unit repeat is duplicated by mirroring on its edges.
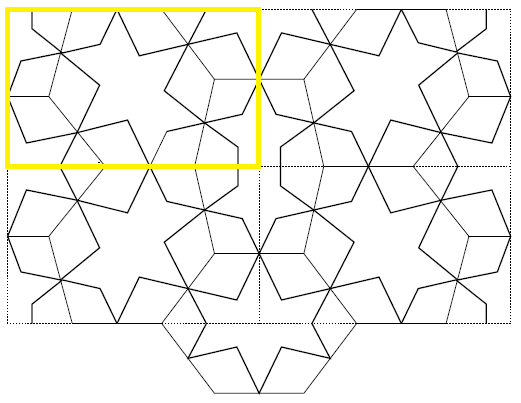
The two hexagonal underlying tiles aren’t visible in the realised pattern. They aren’t created as separate clay tiles or cut out ones. Eventually once the unit repeat is created you don’t even need them to realise the tiling since you just can duplicate the unit repeat. This makes the role of the underlying polygonal pattern un clear and researchers disagree on it. What is clear is the fact that the tiling is created in function of the
area that has to be covered.
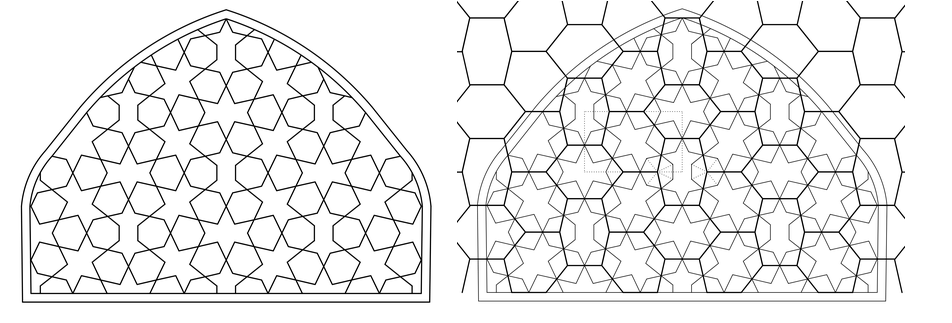
Starting from the apex to the base you see how the standing pointed polygons follow the edge of the arc to the base. You can see as well that the slanted polygons incline according to the edge to the apex. Although there isn’t an exact compass construction for a heptagon, the decorators manage to introduce heptagons in a very natural way into an arc, by using just two types of underlying hexagonal polygons. Above all it’s this contradictory 'creative virtuoso ease' of the designers that is amazing and inviting to study these medieval patterns.