Parábolas y telescopios
En la República Domincana se llama coloquialmente parábolas a las antenas de televisión.
Desde una perspectiva más matemática, la parábola es una de las curvas cónicas.
Se trata de una curva simétrica respecto a un eje, con la propiedad de que cada punto de la curva está a la misma distancia, tanto de un punto llamado foco, como de una recta fija llamada directriz.
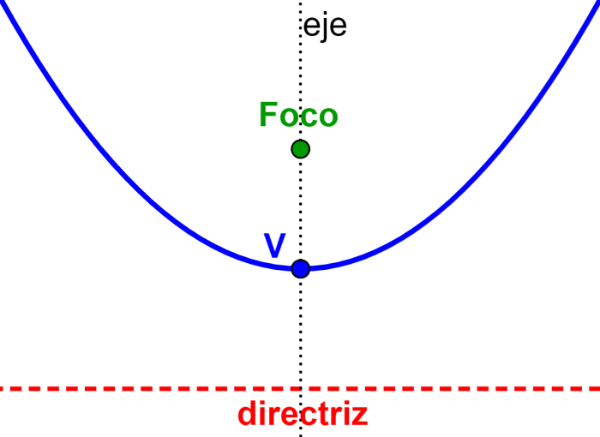
Aunque la forma más sencilla de expresar una parábola en un sistema de coordenadas es:
y=ax2+bx+c
es muy útil utilizar la conocida como forma general
y=a(x-h)2+k
Con la ecuación expresada de esta forma, el eje de simetria de la parábola pasa por x=h, mientras que el vértice está en la posición (h,k), justamente entre el foco y la directriz.
El foco está en la posición (h,k+1/4a) y la directriz es la recta y=k-1/4a, por lo que la distancia entre el foco y la directriz es 1/2a.
En la imagen se puede ver la gráfica de una parábola y su ecuación expresada de las dos formas que se han visto hasta ahora.
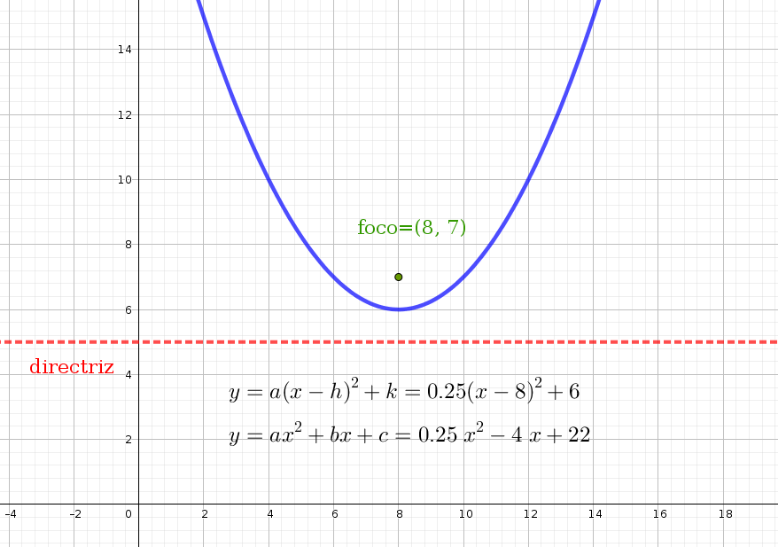
Aunque en esta actividad se van a tratar parábolas abiertas hacia arriba, en caso de que la parábola estuviera abierta hacia la derecha la ecuación tendría la misma forma cambiando x por y, pero también k por h. En ese caso la directriz sería una recta paralela al eje y.
x=a(y-k)2+h
Para la parábola de la imagen anterior:
Actividad 1. Determinar la posición del vértice
Actividad 2. ¿Cuál es la distancia entre el foco y el vértice?
Actividad 3. ¿Cuál es la distancia entre el foco y la directriz?
Actividad 4. Calcular el valor del parámetro a para una parábola cuya distancia entre el foco y la directriz sea de 0.5
Una de las propiedades que define la parábola es que todos los puntos que forman parte de ella están a la misma distancia del foco que de la directriz.
En la siguiente hoja dinámica se puede ver como todos los puntos de la parábola cumplen esta condición. Esto se puede comprobar moviendo el punto E por la parábola.
Actividad 5. ¿Cuáles son los dos puntos de la parábola anterior cuya distancia al foco y a la directriz es igual a 2?
La parábola tiene también otras propiedades menos conocidas. Una propiedad muy útil en la práctica es que todas las rectas perperdiculares a la directriz pasan por el foco al reflejarse en la parábola.
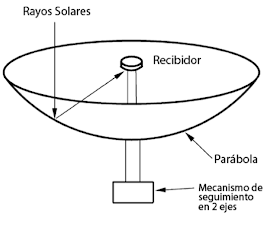
De esta forma se concentran todos los rayos que vienen perpendiculares en un solo punto. Esto produce una amplificación de la señal, por eso muchas antenas, telescopios y concentradores solares tienen forma parabólica.
La idea es colocar un receptor en el foco, de manera que se concentren las señales recibidas desde todos los puntos de la superficie de la antena. Las antenas astronómicas tienen además un sistema de posicionamiento de dos ejes que permite seguir a los objetos en el cielo, por ejemplo una estrella o constelación.
En la siguiente hoja dinámica se muestra como todos los rayos que tienen dirección vertical, van a parar al foco después de rebotar en la parábola. Se puede mover el punto E para ver como esto sucede para cualquier punto de la parábola.
Precisamente debido a esta propiedad es conveniente que los telescopios, concentradores solares o antenas tengan forma parabólica.
En la imagen se pueden ver telescopios del observatorio astronómico ALMA, en Chile.
