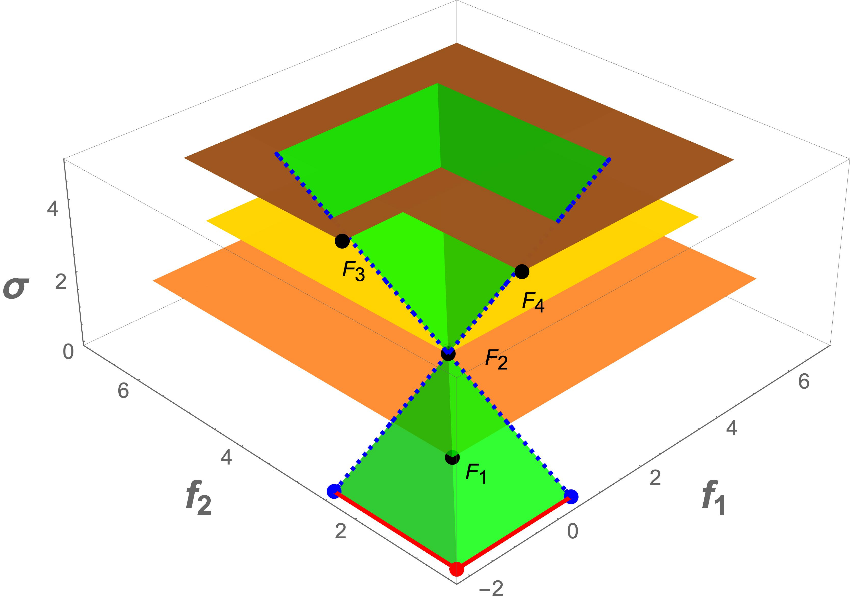
Simple example with Four Points
Potential Pareto Optimality for four hyperintervals on different $\sigma$-levels.
In this example, for every value of $\alpha_1$ and $\alpha_2$ the virtual lower bound for $F_2$ is dominated by the virtual lower bound for one of $F_1$, $F_3$ and $F_4$. Therefore $F_2$ is not Potentially Pareto Optimal.
Figure 6(d) of "On the Extension of the DIRECT Algorithm to Multiple Objectives" by A. Lovison and K. Miettinen.