Übung Pythagoras im Raum
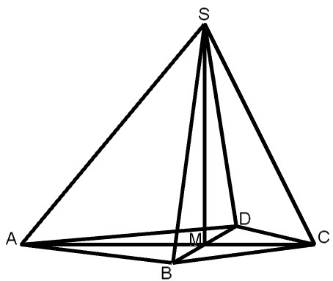
Das Drachenviereck ABCD ist die Grundfläche der Pyramide ABCDS mit der Höhe .
Das Drachenvierecks ABCD besitzt AC als Symmetrieachse und Punkt M ist der Schnittpunkt der Diagonalen.
Es gilt:
a) Zeichne ein Schrägbild der Pyramide ABCDS. AC ist Schrägbildachse.
Für die Zeichnung gilt: q = 0,5; =45°
b) Vom Punkt E ist bekannt: . Berechne die Länge der Strecke und zeichne den Punkt E in das Schrägbild ein.
c) Begründe die Aussage: "Die Strecke erscheint im Schrägbild in wahrer Größe."
d) Die Strecke mit und ist parallel zur Strecke . Der Punkt E ist Mittelpunkt der Strecke . Zeichne die Strecke in das Schrägbild ein.
e) Berechne den Flächeninhalt des Trapez BDGF.
f) Das Trapez BDGF ist Grundfläche der Pyramide BDGFC. Nimm Stellung zur Aussage:
"Die Strecke ist die Höhe der Pyramide BDGFC mit der Grundfläche BDGF."
In diesem Applet kannst du die Lösung Schritt für Schritt durchklicken:
Hilfestellung:
Link zu den Pyramiden im 3D-Modell