Medir ángulos-no
¿Cómo se miden los ángulos?
Para medir ángulos se pueden utilizar diferentes unidades:
- la más empleada en la vida cotidiana es el grado sexagesimal (°): arco cuya longitud es la tricentésima sexagésima (1/360) parte de una circunferencia
- también es utilizada sobre todo por los topógrafos la centesimal (g): arco cuya longitud es la cuadringentésima (1/400) parte de una circunferencia.
-por los matemáticos el radian.
Desde 1995 el radián, junto con el estereoradián son unidades del Sistema Inernacional de Unidades que figuran en la categoría de unidades derivadas
Esta unidad se utiliza primordialmente en física, cálculo infinitesimal, trigonometría o goniometría.
¿Pero qué es exactamente un radián?
Un radián es el ángulo central de una circunferencia que abarca un arco de igual longitud que el radio de la misma.
¡Qué complicado ! ¿Y si pruebas a construirlo tú mismo?
Mueve el punto E hasta que la longitud del arco sea 1Crea tu propio radián
¿ Y si la circunferencia en lugar de radio 1, tiene un radio diferente?
Utiliza el deslizador que marca el ángulo hasta que la longitud del arco sea igual al radio Puedes probar con diferentes radios, a ver que pasa
Crea tu propio radián
¿ Lo has conseguido? ¡ Perfecto, eso es un radián !
La equivalencia entre grados sexagesimales y radianes es: π rad = 180°.
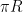(como todos deberíamos saber), entonces tenemos lo siguiente:
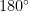ya tenemos nuestra relación:
Por tanto 1 radián = 57.29577951... grados sexagesimales y al revés 1 grado sexagesimal = 0.01745329252... radianes.
Veamos. En general, la medida en radianes de un ángulo en una circunferencia es igual a la longitud del arco que abarca dividida entre el radio de dicha circunferencia:
(como todos deberíamos saber), entonces tenemos lo siguiente:
ya tenemos nuestra relación: 
Fíjate bien: ¿ Cambia el ángulo según calcules el radián en una circunferencia con r= 1, o una circunferencia con r= 5 ? * Ten en cuenta que puede variar algo por el margen de tolerancia de geogebra*
¿Entonces a cuántos radianes corresponderán a la circunferencia completa de 360º?
Lucas V. Barbosa [Public domain]
¿por qué cuando usamos funciones trigonométricas en cálculo solemos trabajar con radianes?
Pues como dicen en la página de la Wikipedia en inglés dedicada al radián: porque las expresiones de muchos resultados quedan mucho mejor si trabajamos en radianes.
en radianes conservamos este bonito límite:
:
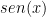Los radianes poseen una “naturalidad” matemática que lleva a una formulación más elegante de unos cuantos resultados importantes.Por ejemplo, si expresamos
en radianes conservamos este bonito límite:
:
