원뿔곡선: 타원과 쌍곡선의 초점
본 학습 자료는 『Modern Geometry with Applications』 (George A. Jennigs)의 내용을 바탕으로 만들었습니다.
원뿔곡선의 초점에 대한 성질은 실제 응용에서 상당히 중요하다. 최소한 그리스의 기하학자 아폴로니우스(기원전 262-190) 때부터 이를 연구하였다. 우리는 1822년 벨기에의 수학자 G. P. Dandelin이 발견한 구를 이용한 방법으로 이 성질을 탐구하고자 한다.
Dandelin은 원뿔 에 내접하고 평면 에 접하며 중심이 원뿔의 축 위에 있는 구를 이용하였다. 타원이나 쌍곡선은 평면 에 접하며 원뿔의 내접하는 구는 두 개가 있으며, 포물선은 하나의 구만 존재한다. 먼저 타원과 쌍곡선의 초점에 대해 알아보자.
원뿔 에 내접하고 평면 에 접하는 구를 , 라 하고, 구 , 가 평면 와 접하는 점을 각각 , 라 하자.
명제(타원의 초점에 대한 성질)
타원 위의 임의의 점 에 대하여 의 값은 항상 일정하다.
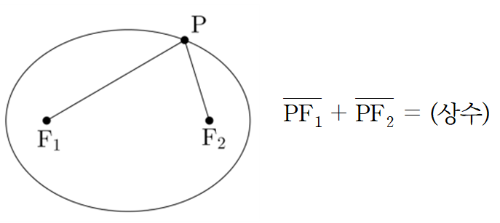
점 P를 움직여보며 수학적 사실을 찾아보세요.
위에서 관찰한 수학적 사실을 모두 작성해보세요.
위에 작성한 내용을 바탕으로 타원 위의 임의의 점에서 두 점 , 까지의 거리의 합이 같은 이유를 작성해보세요.
명제(쌍곡선의 초점에 대한 성질)
쌍곡선 위의 임의의 점 에 대하여 의 값은 항상 일정하다.
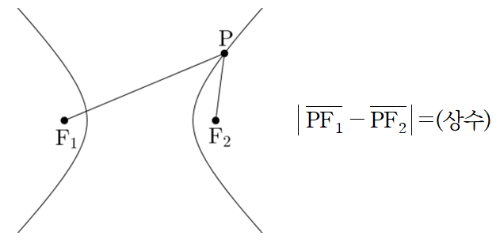
점 P를 움직여보며 수학적 사실을 찾아보세요.
위에서 관찰한 수학적 사실을 모두 작성해보세요.
위에 작성한 내용을 바탕으로 쌍곡선 위의 임의의 점에서 두 점 , 까지의 거리의 차가 같은 이유를 작성해보세요.