Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Gli angoli sulla circonferenza

Autore:Ilic Ferretti
Una parte importante delle proprietà di una circonferenza riguardano gli angoli che si possono costruire su di essa e le loro proprietà. Vediamo alcune definizioni ed una proprietà fondamentale, nella prossima animazione.
Riassumendo, il teorema appena visto ci garantisce che:
  • un angolo alla circonferenza è sempre pari alla metà dell'angolo al centro che insiste sullo stesso arco.
  • ne consegue che tutti gli angoli alla circonferenza che insistono sullo stesso arco sono uguali (sono la metà dello stesso angolo al centro)
Vogliamo utilizzare questa proprietà per studiare le proprietà dei triangoli, ed in particolare dei loro angoli. Ma cosa centrano i triangoli con le circonferenze? Lo vediamo nel prossimo paragrafo. TUTTI I TRIANGOLI SONO INSCRIVIBILI IN UNA CIRCONFERENZA Dimostriamo allora che qualsiasi triangolo può sempre essere circoscritto in una circonferenza, ovvero che esiste sempre una circonferenza che passa per i suoi tre vertici.
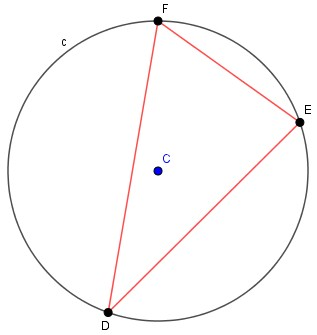
Il triangolo DEF si dice INSCRITTO nella circonferenza c perchè i suoi tre vertici le appartengono. La circonferenza si dice CIRCOSCRITTA al triangolo.
Il triangolo DEF si dice INSCRITTO nella circonferenza c perchè i suoi tre vertici le appartengono. La circonferenza si dice CIRCOSCRITTA al triangolo.
La dimostrazione è articolata in due parti
  1. Conosciamo già l'elemento più importante della dimostrazione: é l'asse di un segmento, i cui punti come sappiamo sono equidistanti dagli estremi del segmento (questo dovrebbe ricordarci molto la circonferenza, perché anche i suoi punti sono tutti equidistanti, in questo caso dal centro della circonferenza stessa). L'asse di un segmento è stato uno dei primi luoghi geometrici che abbiamo studiato, e prima di proseguire puoi ripassarlo a questo indirizzo: https://www.geogebra.org/m/sV6phd5z#material/UaK8Sc8t
  2. A questo punto dobbiamo dimostrare che gli assi di un triangolo (cioè dei suoi tre lati) si incontrano sempre tutti nello stesso punto; lo puoi vedere qui: https://www.geogebra.org/m/sV6phd5z#material/TzB6iWKp; in questa stessa dimostrazione viene detto e spiegato che tale punto di incontro si chiama CIRCOCENTRO, proprio perchè è il centro della circonferenza circoscritta al triangolo.
Abbiamo quindi dimostrato che ogni triangolo, avendo un circocentro, può essere inscritto in una circonferenza. C.V.D. I TRIANGOLI INSCRITTI IN UNA SEMICIRCONFERENZA SONO RETTANGOLI A questo punto vediamo un'ultima proprietà piuttosto curiosa: tutti i triangoli inscritti in una semicirconferenza sono rettangoli. Lo dimostriamo nell'animazione qui sotto.
Questa importantissima proprietà è essenziale per dimostrare una legge fondamentale della trigonometria, detta "teorema dei seni". Proseguiamo quindi il discorso nel geogebra book dedicato alle funzioni trascendenti, ed in particolare al capitolo sulle relazioni goniometriche e trigonometriche avanzate, in questa pagina: https://www.geogebra.org/m/XJmWSY7D

Nuove risorse

Scopri le risorse

Scopri gli argomenti