Asimmetria nel paradosso dei gemelli

Twin paradox asymmetry
Mentre tra due riferimenti inerziali la trasformazione è affine (semplice da immaginare: tempi e spazi sono proporzionali) un riferimento non inerziale è caratterizzato non da una singola trasformazione, ma da una infinità di trasformazioni affini legate tra loro da una legge.
Se queste infinite trasformazioni le prendiamo come un tutto (*), allora ad ogni evento di un riferimento inerziale, corrisponderanno infinite rappresentazioni in quello non inerziale, uno per ogni nuovo riferimento individuato dal tempo proprio cdi K', originato dal cambiamento di velocità.
Uno stesso evento si trasformerà in una traiettoria nello spaziotempo nel nuovo "insieme di riferimenti K'()", ovvero - in parole forse più adeguate - lo stesso evento cambierà, nel corso del tempo proprio, rappresentazione, collocazione.
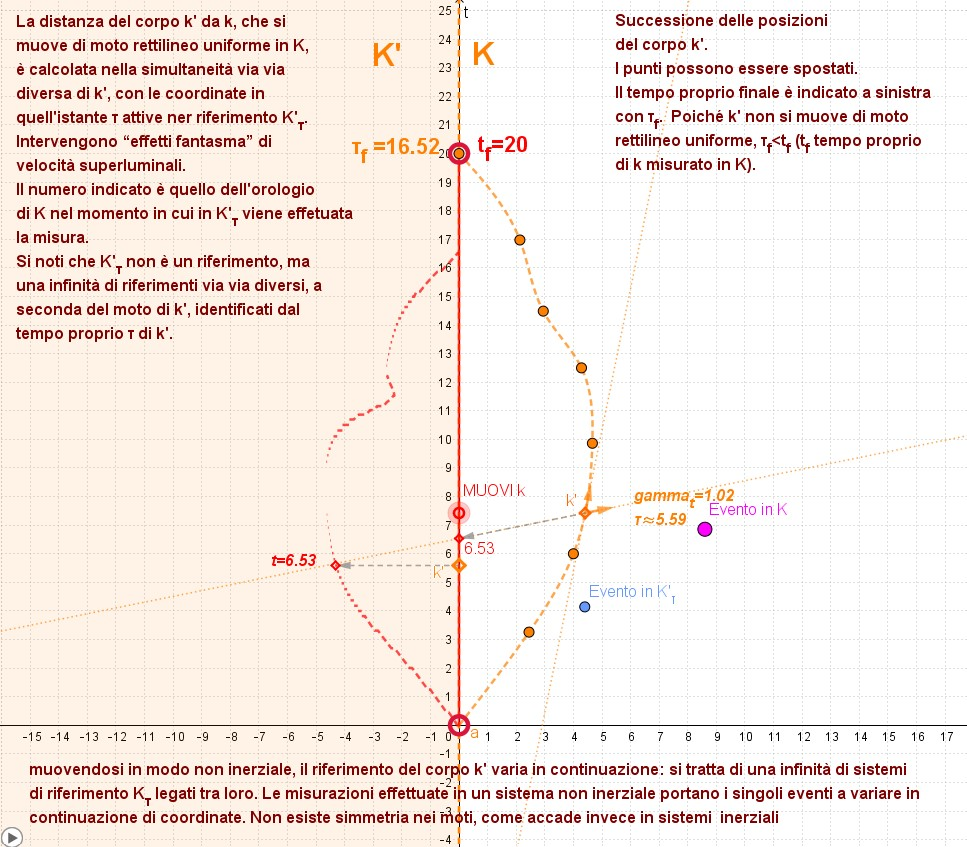
Se poi prendiamo un corpo che nel sistema inerziale si muove con legge x=0 (s-luce/s * s), ovvero il corpo k che resta fermo nell'origine mentre il tempo passa, la sua posizione "nei" K' dovrà essere presa nella contemporaneità di quell'istante di tempo proprio per il corpo k'.
Siccome le "alette" (i versori degli assi nel K'() di ogni istante) si aprono e chiudono in continuazione, questa posizione (intersezione della giacitura del versore di x' con l'asse x=0) sarà presa in tempi che possono variare anche con estrema rapidità: fenomeno "illusorio".
Una simile illusione la possiamo avere quando giriamo la testa e affermiamo erroneamente che sia il sole a girarsi con una velocità superiore a quella della luce.
Quindi due aspetti di asimmetria: mancata rappresentazione univoca degli eventi e fenomeni "fantasma" nell'osservazione di un moto rettilineo uniforme.
Furio Petrossi
---
(*) La rappresentazione mentale non è immediata. Geometricamente, usando un sistema di riferimento cartesiano, ad esempio, si suole rappresentare sul piano (x,t) anche il piano (x',t') con una griglia "affine" per rappresentare le coordinate degli stessi eventi nel sistema di riferimento K' (qui sistema cartesiano, non solo riferimento).
Ebbene, qui abbiamo una infinità di "griglie" affini individuate dal parametro "tau", tempo proprio di K', griglie che potrebbero essere rappresentate ad esempio in una ulteriore terza dimensione "impilandole" come (x'(),t'()).
In alternativa, possiamo immaginare una griglia che varia la sua struttura nel tempo, soluzione che ho preferito usare nel foglio dinamico.
Vedere anche
https://www.geogebra.org/m/qnh59yx6 ("paradosso" dei gemelli)
SRCalc (Calcolatrice Relatività ristretta)
https://www.geogebra.org/m/wqf5bEum (due piani affiancati)
https://www.geogebra.org/m/XNzUyQcp (unico piano)
https://www.geogebra.org/m/TFWVAWk7 (composizione velocità)
https://www.geogebra.org/m/N2Rybc85 (orologio a luce e calcolo di gamma)
https://www.geogebra.org/m/qnh59yx6 ("paradosso" dei gemelli)
https://www.geogebra.org/m/rub85zpx (asimmetrie nel paradosso dei gemelli) *** questo foglio ***