Circoscritti a una circonferenza
Un poligono è inscritto in una circonferenza quando tutti i suoi
vertici appartengono alla circonferenza.
La circonferenza è circoscritta al poligono.
Quando un poligono è inscritto in una circonferenza, il centro
della circonferenza coincide con il circocentro del poligono
(punto d’incontro degli assi del poligono).
Un poligono è circoscritto in una circonferenza quando tutti i
suoi lati sono tangenti alla circonferenza.
La circonferenza è inscritta al poligono.
Quando un poligono è circoscritto in una circonferenza, il centro
della circonferenza coincide con l’incentro del poligono (punto
d’incontro delle bisettrici degli angoli del poligono).
Condizioni di circoscrivibilità:
Un poligono è circoscrittibile in una circonferenza se le bisettrici
dei suoi angoli s’incontrano in un unico punto, detto incentro del
poligono.
Un quadrilatero è circoscrittibile in una circonferenza se la somma
delle misure dei lati opposti sono uguali.
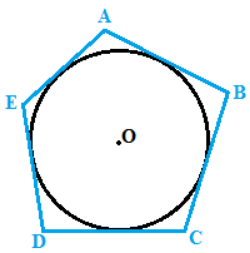
![Disegniamo ora le distanze dei lati del poligono dal centro della circonferenza.
Ovviamente i segmenti [i]OQ[/i], [i]OK[/i], [i]OP[/i], [i]ON[/i], [i]OH[/i] sono congruenti essendo i RAGGI della circonferenza. Quindi i lati del poligono sono tutti equidistanti dal centro della circonferenza.
Ora, dallo studio dei triangoli abbiamo appreso che l'[url=http://www.lezionidimatematica.net/Triangoli/lezioni/triangoli_lezione_15.htm]i[/url]ncentro è equidistante dai lati.
Ricordiamo che l'incentro è il punto in cui si incontrano le bisettrici di un poligono e che per bisettrice di un angolo si intende la semiretta che ha per origine il vertice dell'angolo e che divide l'angolo in due parti uguali.
Quindi, nel nostro poligono circoscritto l'incentro, che è il punto equidistante dai lati del poligono, coincide con il centro della circonferenza.
Esse si incontrano nel punto[i] O[/i] che rappresenta l'incentro, ma che è anche il centro della circonferenza.
[color=#000000]Quindi possiamo dire che un poligono [/color][color=#000000]si può [/color]circoscrivere[color=#000000] a una [/color]circonferenza[color=#000000] [/color]se le bisettrici di tutti i suoi angoli si incontrano tutte in un unico punto che è anche il centro della circonferenza.](https://stage.geogebra.org/resource/bpsEKmE6/KCYkUb2HJN7NiImL/material-bpsEKmE6.png)