Sobre Telescopios, Antenas y Parábolas

Considera el corte transversal de un espejo con forma de parábola, llamemos a dicha parábola , que tiene como directriz la recta y como foco u punto . Pensemos en la situación donde disparamos haces de luz en dirección perpendicular a hacia la parábola . Los espejos reflejan la luz, entonces los haces "rebotaran" cuando lleguen a la parábola . La cuestión es: ¿todos estos haces de luz que rebotan de la parábola H inciden en un mismo punto?, si es así, ¿en qué punto lo hacen?

Primero veamos la noción de tangente a una parábola en un punto dado. La parábola H divide al plano en dos regiones, la que está “dentro” de la parábola (donde está el foco ) y la que está afuera (donde esta el la directriz ). Una recta es tangente a la parábola en el punto si su única intersección con la parábola H es P y la recta T esta “fuera” de la parábola . Ahora, el ángulo de incidencia de un haz de luz es el ángulo que forma el haz de luz con la tangente al punto donde choca cuando el haz de luz llega al espejo. Análogamente, el ángulo de reflexión es el ángulo que forma el haz de luz con la tangente al punto donde choca cuando él haz sale del espejo. Un hecho físico útil en este contexto es que el ángulo de incidencia es igual al ángulo de reflexión. Esto se deduce del Principio de Fermat, que en palabras simples dice que la luz toma trayectorias que minimicen el tiempo de recorrido.

Veamos primero cómo construir la tangente de una parábola en un punto dado cuando conocemos el foco y la directriz de la parábola .

El segmento es perpendicular a , entonces . Recordemos que el lugar geométrico de la parábola con foco y directriz es el conjunto         {}. Además, , pues está en y , pues es perpendicular a . Por lo tanto, , lo que significa que está en , es decir, está en la intersección de y . Sea cualquier punto en la intersección de y . Como está en , tenemos que . Puesto que está en , se sigue que y por ende Recuerdemos que está en y la distancia de un punto a una recta es la distancia de dicho punto al pie de la perpendicular (qué pasa por dicho punto) a la recta, por lo tanto es perpendicular a . Sin embargo, es también perpendicular a , por lo tanto . Por lo que la intersección de y única. Adicionalmente, resulta que T esta “fuera” de la parábola , entonces es la tangente a la parábola en el punto . Por lo tanto, todos los haces de luz que se reflejan de la parábola , inciden en el foco .

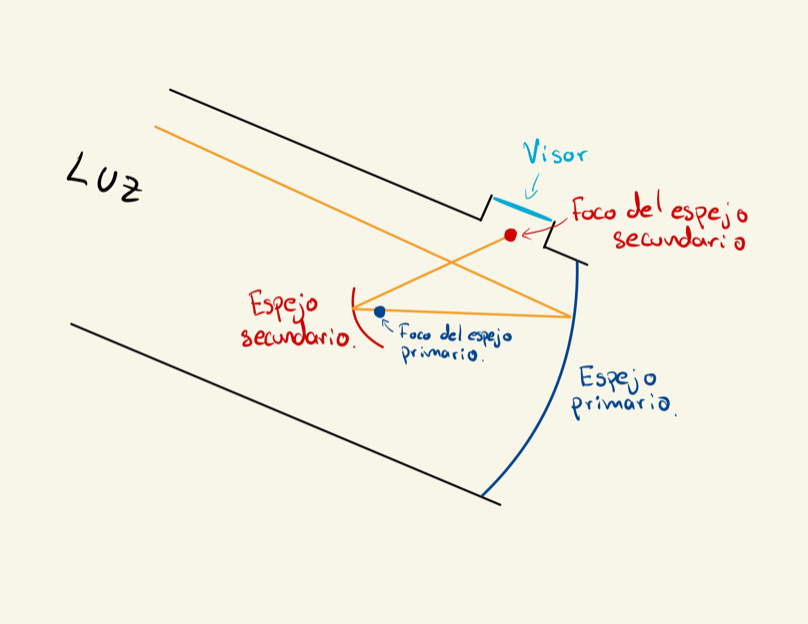
La propiedad de incidencia en el foco es usada en la estructura básica de los telescopios. La estructura de una antena es: un espejo primario, cuyos cortes transversales tienen forma de parábola, lo cual hace que la luz se refleje y pase por el foco de las parábolas que son cortes transversales medios del espejo primario. En dicho foco se pone otro espejo secundario, cuyos cortes transversales tienen de nuevo forma de parábola, en el cual la luz rebota hacia el foco de las parábolas que son cortes transversales medios del espejo secundario, donde se coloca un visor, en el cual el ojo humano capta la luz.

Curiosidad: No sólo la luz tiene la propiedad de incidencia en el foco. Las ondas de sonido y las ondas electromagnéticas se comportan de esta forma también. Esto se utiliza mucho en las telecomunicaciones. En el Centro de Ciencias Matemáticas, ubicado en Morelia, se encuentran dos antenas parábolicas ubicadas una enfrente de la otra. Lo curioso es que si dos personas se paran en el foco de cada antena y hablan, se escuchan como si estuvieran extremadamente cerca. Esto pasa pues las ondas de sonido chocan la superficie de las antenas, rebotan e inciden en el foco.